
 如图,在Rt△OAB中,∠B=Rt∠,OB=2AB.线段AB的垂直平分线交反比例函数y=
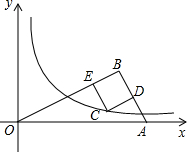
如图,在Rt△OAB中,∠B=Rt∠,OB=2AB.线段AB的垂直平分线交反比例函数y= (x>0)的图象于点C,D为垂足,过C作CE⊥OB于点E.当四边形CDBE为正方形时,正方形CDBE的面积为________.
(x>0)的图象于点C,D为垂足,过C作CE⊥OB于点E.当四边形CDBE为正方形时,正方形CDBE的面积为________.
 OB=2a,则FC=2a-a=a,于是CP为△FDA的中位线,CP=
OB=2a,则FC=2a-a=a,于是CP为△FDA的中位线,CP= AD=
AD= a,在Rt△CFP中,根据勾股定理计算出PF=
a,在Rt△CFP中,根据勾股定理计算出PF= a,利用面积法计算出CH=
a,利用面积法计算出CH= a,在Rt△CFH中,根据勾股定理计算HF=
a,在Rt△CFH中,根据勾股定理计算HF= a,OA=2
a,OA=2 a,所以OF=
a,所以OF= OA=
OA= a,则可确定C点坐标为(
a,则可确定C点坐标为(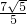 a,
a, a),然后把C点坐标代入反比例解析式得到a2.
a),然后把C点坐标代入反比例解析式得到a2.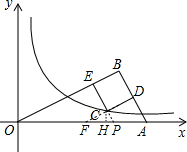
 OB=2a,
OB=2a, AD=
AD= a,
a,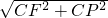 =
= a,
a, CH•PF=
CH•PF= CP•CF,即
CP•CF,即 CH•
CH• a=
a= a•
a• a,
a, a,
a,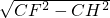 =
= a,
a,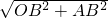 =2
=2 a,
a, OA=
OA= a,
a,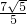 a,
a,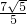 a,
a, a),
a),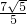 a,
a, a)代入y=
a)代入y= 得
得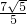 a•
a• a=2,解得a2=
a=2,解得a2= .
. .
.

 新课标同步训练系列答案
新课标同步训练系列答案科目:初中数学 来源: 题型:
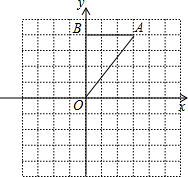 如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:
 OA1B1.
OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
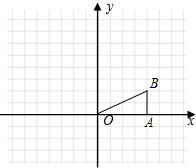
 如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com