
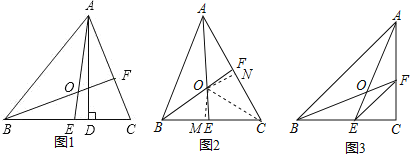
【题目】在△ABC 中,AE、BF 是角平分线,交于 O 点.
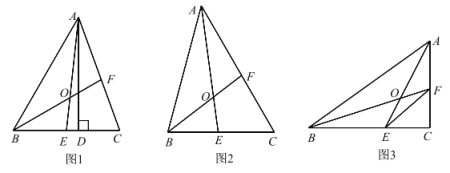
(1)如图 1,AD 是高,∠BAC=90°,∠C=70°,求∠DAC 和∠BOA 的度数;
(2)如图 2,若 OE=OF,求∠C 的度数;
(3)如图 3,若∠C=90°,BC=8,AC=6,S△CEF=4,求 S△AOB.
【答案】(1)∠DAC=20°,∠BOA=125° (2)60° (3)10
【解析】
(1)根据垂直的定义得到∠ADC=90°,根据角平分线的定义得到∠ABO=30°,根据三角形的内角和即可得到结论;
(2)连接OC,根据角平分线的性质得到OM=ON,根据全等三角形的性质得到∠EOM=∠FOH,根据角平分线的定义即可得到结论;
(3)根据勾股定理得到AB=![]() =10,根据三角形的面积公式得到CF,求得AF,得到S△ABF=S△ABC-S△BCF,根据角平分线定理得到
=10,根据三角形的面积公式得到CF,求得AF,得到S△ABF=S△ABC-S△BCF,根据角平分线定理得到![]() ,求得
,求得![]() =3,于是得到结论.
=3,于是得到结论.
(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°-90°-70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°;
(2)如图2:连接OC,
∴AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,
![]() ,
,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°-∠C,
∵AE、BF是角平分线,
∴∠AOB=90°+![]() ∠ACB,
∠ACB,
即90°+![]() ∠ACB=180°-∠ACB,
∠ACB=180°-∠ACB,
∴∠ACB=60°;
(3)∵∠C=90°,BC=8,AC=6,
∴AB=![]() =10,
=10,
∵AE是角平分线,
∴![]() ,
,
∴BE=5,CE=3,
∵S△CEF=![]() ECCF=
ECCF=![]() ×3CF=4,
×3CF=4,
∴CF=![]() ,
,
∴AF=![]() ,
,
∵S△ABC=![]() BCAC=
BCAC=![]() ×8×6=24,
×8×6=24,
∴S△ABF=S△ABC-S![]() ×8×
×8×![]() =
=![]()
∵AE平分∠BAC,
∴![]()
∴![]() =3,
=3,
∴![]()
∴S△AOB=![]() =10.
=10.


科目:初中数学 来源: 题型:
【题目】已知,Rt△ABC中,∠C=90.
(1)当∠B=60时,![]() =_______;当∠A=45时,
=_______;当∠A=45时,![]() =_______.
=_______.
(2)当∠B=2∠A时,求![]() 的值;
的值;
(3)若AB=2BC,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
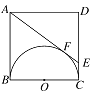
【题目】如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象抛物线与
的图象抛物线与![]() 轴相交于不同的两点
轴相交于不同的两点![]() ,
,![]() ,且
,且![]() ,
,
(1)若抛物线的对称轴为![]() 求的
求的![]() 值;
值;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若该抛物线与![]() 轴相交于点D,连接BD,且∠OBD=60°,抛物线的对称轴
轴相交于点D,连接BD,且∠OBD=60°,抛物线的对称轴![]() 与
与![]() 轴相交点E,点F是直线
轴相交点E,点F是直线![]() 上的一点,点F的纵坐标为
上的一点,点F的纵坐标为![]() ,连接AF,满足∠ADB=∠AFE,求该二次函数的解析式.
,连接AF,满足∠ADB=∠AFE,求该二次函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你用树状图或列表法列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
①画线段AB;
②画射线CA、直线AD;
③过点B画AD的平行线BE;
④过点D画AC的垂线,垂足为F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了解政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1、图2.

小明发现每月每户的用水量为5 ![]() -35
-35 ![]() 之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
(1)![]() ,小明调查了 户居民,并补全图1;
,小明调查了 户居民,并补全图1;
(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com