练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知，Rt△ABC中，∠C=90.

    （1）当∠B=60时，=_______；当∠A=45时，=_______.

    （2）当∠B=2∠A时，求的值；

    （3）若AB=2BC，求∠A的度数.

    【答案】（1），1（2）（3）30°

    【解析】

    （1）根据三角函数的定义即可求出在Rt△ABC中，当∠B=60时的值和∠A=45时的值.

    （2）根据∠C=90，∠B=2∠A可求得∠A 的度数，后根据三角函数的定义可求出的值.

    （3）根据∠C=90，AB=2BC， 可求出的值，后根据反三角函数的定义可求出∠A的度数.

    （1）在 Rt△ABC中，∠C=90,

    当∠B=60时，

    在Rt△ABC中，∠C=90

    ∠A=45时，

    （2）在 Rt△ABC中，∠C=90, ∠B=2∠A

    即

    （3）在 Rt△ABC中，∠C=90，AB=2BC

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

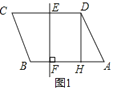
    【题目】如图，△ABC与△DCE有公共顶点C，AB=CD，BC=CE，∠ABC=∠DCE=90°.

    （1）如图1，当点D在BC延长线上时.

    ①求证：△ABC≌△DCE.

    ②判断AC与DE的位置关系，并说明理由.

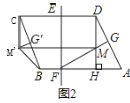
    （2）如图2，△CDE从（1）中位置开始绕点C顺时针旋转，当点D落在BC边上时停止.

    ①若∠A=60°，记旋转的度数为，当为何值时，DE与△ABC一边平行.

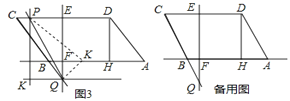
    ②如图3，若AB=c， BC=a， AC=b， a>c，边BC，DE交于点F，求整个运动过程中，F在BC上的运动路程（用含a， b， c的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=﹣（x﹣h）2（h为常数），当自变量x的值满足2≤x≤5时，与其对应的函数值y的最大值为﹣1，则h的值为（ ）

    A. 3或6 B. 1或6 C. 1或3 D. 4或6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在ABCD中，DH⊥AB于点H，CD的垂直平分线交CD于点E，交AB于点F，AB=6，DH=4，BF：FA=1：5．

    （1）如图2，作FG⊥AD于点G，交DH于点M，将△DGM沿DC方向平移，得到△CG′M′，连接M′B．

    ①求四边形BHMM′的面积；

    ②直线EF上有一动点N，求△DNM周长的最小值．

    （2）如图3，延长CB交EF于点Q，过点Q作QK∥AB，过CD边上的动点P作PK∥EF，并与QK交于点K，将△PKQ沿直线PQ翻折，使点K的对应点K′恰好落在直线AB上，求线段CP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】21．（2013年四川攀枝花8分）某文具店准备购进甲，乙两种铅笔，若购进甲种钢笔100支，乙种铅笔50支，需要1000元，若购进甲种钢笔50支，乙种钢笔30支，需要550元．

    （1）求购进甲，乙两种钢笔每支各需多少元；

    （2）若该文具店准备拿出1000元全部用来购进这两种钢笔，考虑顾客需求，要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍，且不超过乙种钢笔数量的8倍，那么该文具店共有几种进货方案；

    （3）若该文具店销售每支甲种钢笔可获利润2元，销售每支乙种钢笔可获利润3元，在第（2）问的各种进货方案中，哪一种方案获利最大；最大利润是多少元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，已知点D，E，F分别为BC，AD，AE的中点，且S△ABC=4cm2，则阴影部分面积S=（　　）cm2．

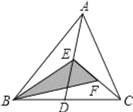
    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）解方程： －＝－1； （2）解不等式组：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

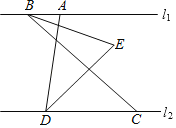
    【题目】如图，已知直线l1∥l2，点A、B在直线l1上，点C、D在直线l2上，点C在点D的右侧，∠ADC＝80°，∠ABC＝n°，BE平分∠ABC，DE平分∠ADC，直线BE、DE交于点E．

    （1）写出∠EDC的度数_____；

    （2）试求∠BED的度数（用含n的代数式表示）；

    （3）将线段BC向右平行移动，其他条件不变，请直接写出∠BED的度数（用含n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC 中，AE、BF 是角平分线，交于 O 点.

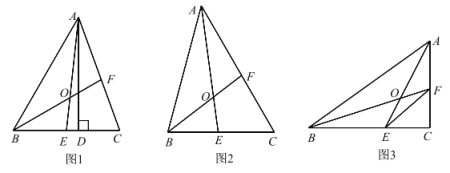
    （1）如图 1，AD 是高，∠BAC＝90°，∠C＝70°，求∠DAC 和∠BOA 的度数；

    （2）如图 2，若 OE＝OF，求∠C 的度数；

    （3）如图 3，若∠C＝90°，BC＝8，AC＝6，S△CEF＝4，求 S△AOB.

    查看答案和解析>>

    同步练习册答案