
【题目】21.(2013年四川攀枝花8分)某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元;
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案;
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大;最大利润是多少元.
【答案】(1)甲,乙两种钢笔每支各需5元和10元;(2)六种;(3)乙钢笔20支,甲钢笔160支时获利最大,最大利润为380元.
【解析】
(1)先设购进甲,乙两种钢笔每支各需a元和b元,根据购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元列出方程组,求出a,b的值即可.
(2)先设购进甲钢笔x支,乙钢笔y支,根据题意列出5x+10y=1000和不等式组6y≤x≤8y,把方程代入不等式组即可得出20≤y≤25,求出y的值即可.
(3)先设利润为W元,得出W=2x+3y=400﹣y,根据一次函数的性质求出最大值.
解:(1)设购进甲,乙两种钢笔每支各需a元和b元,根据题意得:
![]() ,解得:
,解得:![]() .,
.,
答:购进甲,乙两种钢笔每支各需5元和10元.
(2)设购进甲钢笔x支,乙钢笔y支,根据题意可得:
![]() ,解得:20≤y≤25.
,解得:20≤y≤25.
∵x,y为整数,∴y=20,21,22,23,24,25共六种方案.
∵5x=1000﹣10y>0,∴0<y<100.
∴该文具店共有6种进货方案.
(3)设利润为W元,则W=2x+3y,
∵5x+10y=1000,∴x=200﹣2y,代入上式得:W=400﹣y.
∵W随着y的增大而减小,
∴当y=20时,W有最大值,最大值为W=400﹣20=380(元).
即当乙钢笔20支,甲钢笔160支时获利最大,最大利润为380元.


科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠ABC,补充一个条件,使得△ABD≌△ABC,则下列选项不符合题意的是( )
A. ∠D=∠CB. ∠DAB=∠CABC. BD=BCD. AD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
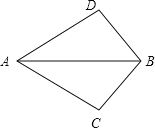
【题目】将长为![]() ,宽为
,宽为![]() 的长方形白纸,按图示方法粘合起来,粘合部分宽为
的长方形白纸,按图示方法粘合起来,粘合部分宽为![]() .
.
(1)根据图示,将下表补充完整;
白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
纸条长度/ | 40 | 110 | 145 | … |
(2)设![]() 张白纸粘合后的总长度为
张白纸粘合后的总长度为![]() ,求
,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)将若干张白纸按上述方式粘合起来,你认为总长度可能为![]() 吗?为什么?
吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
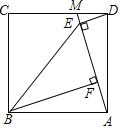
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,Rt△ABC中,∠C=90.
(1)当∠B=60时,![]() =_______;当∠A=45时,
=_______;当∠A=45时,![]() =_______.
=_______.
(2)当∠B=2∠A时,求![]() 的值;
的值;
(3)若AB=2BC,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )

A. 6![]() B. 7
B. 7![]() C. 8
C. 8![]() D. 9
D. 9![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额-成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com