
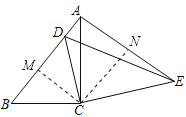
【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )

A. 6![]() B. 7
B. 7![]() C. 8
C. 8![]() D. 9
D. 9![]()
【答案】C
【解析】先解直角△ABC,得出BC=AB×cosB=18×![]() =12,AC=
=12,AC=![]() =6
=6![]() . 再根据旋转的性质得出BC=DC=6,AC=EC=3
. 再根据旋转的性质得出BC=DC=6,AC=EC=3![]() ,∠BCD=∠ACE,利用等边对等角以及三角形内角和定理得出∠B=∠CAE,作CM⊥BD于M,作CN⊥AE于N,则∠BCM=
,∠BCD=∠ACE,利用等边对等角以及三角形内角和定理得出∠B=∠CAE,作CM⊥BD于M,作CN⊥AE于N,则∠BCM=![]() ∠BCD,∠ACN=
∠BCD,∠ACN=![]() ∠ACE,∠BCM=∠ACN,解直角△ANC求出AN=AC×cos∠CAN=6
∠ACE,∠BCM=∠ACN,解直角△ANC求出AN=AC×cos∠CAN=6![]() ×
×![]() =4
=4![]() ,根据等腰三角形三线合一的性质得出AE=2AN=8
,根据等腰三角形三线合一的性质得出AE=2AN=8![]() .
.
解:∵在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,
,
∴BC=AB×cosB=18×![]() =12,AC=
=12,AC=![]() =6
=6![]() .
.
∵把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,
∴△ABC≌△EDC,BC=CD=12,AC=EC=6![]() ,∠BCD=∠ACE,
,∠BCD=∠ACE,
∴∠B=∠CAE.
作CN⊥AE于N,则∠BCM=![]() ∠BCD,∠ACN=
∠BCD,∠ACN=![]() ∠ACE,
∠ACE,
∴∠BCM=∠ACN,
∵在△ANC中,∠ANC=90°,AC=6![]() ,cos∠CAN=cosB=
,cos∠CAN=cosB=![]() ,
,
∴AN=AC×cos∠CAN=6![]() ×
×![]() =4
=4![]() ,
,
∴AE=2AN=8![]() .
.
故答案为:8![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
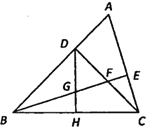
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
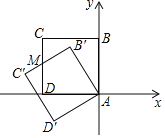
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】21.(2013年四川攀枝花8分)某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元;
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案;
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大;最大利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.
(1)试分析28是否为“神秘数”;
(2)下面是两个同学演算后的发现,请选择一个“发现”,判断真、假,并说明理由.
①小能发现:两个连续偶数2k+2和2k(其中k取非负整数)构造的“神秘数”也是4的倍数.
②小仁发现:2016是“神秘数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB∥CD,点P在其所在平面上,且不在直线AB,CD,AC上,设∠PAB=α,∠PCD=β,∠APC=γ(α,β,γ,均不大于180°,且不小于0°).
(1)如图1,当点P在两条平行直线AB,CD之间、直线AC的右边时试确定α,β,γ的数量关系;
(2)如图2,当点P在直线AB的上面、直线AC的右边时试确定α,β,γ的数量关系;
(3)α,β,γ的数量关系除了上面的两种关系之外,还有其他的数量关系,请直接写出这些.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》里有一道著名算题:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二乘、问上、下禾实一乘各几何?”大意是:3捆上等谷子结出的粮食,再加.上六斗,相当于10捆下等谷子结出的粮食.5捆下等谷子结出的粮食,再加上一斗,相当于2捆上等谷子结出的粮食.问:上等谷子和下等谷子每捆能结出多少斗粮食?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(5,0),B(0,5).
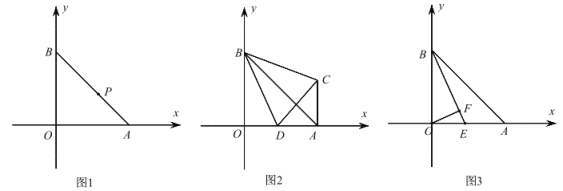
(1)如图 1,P 是 AB 上一点且![]()
![]() ,求 P 点坐标;
,求 P 点坐标;
(2)如图 2,D 为 OA 上一点,AC∥OB 且∠CBO=∠DCB,求∠CBD 的度数;
(3)如图 3,E 为 OA 上一点,OF⊥BE 于 F,若∠BEO=45°+∠EOF,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com