
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.
(1)试分析28是否为“神秘数”;
(2)下面是两个同学演算后的发现,请选择一个“发现”,判断真、假,并说明理由.
①小能发现:两个连续偶数2k+2和2k(其中k取非负整数)构造的“神秘数”也是4的倍数.
②小仁发现:2016是“神秘数”.
【答案】(1)28是“神秘数”(2)①是4的倍数,且是奇数倍②2016不是“神秘数”
【解析】
(1)根据题意设未知数x,列出对应方程x2-(x-2)2=28,求解即可.
(2)根据小能的发现列式:(2k+2)2-(2k)2化简,观察化简后的式子是否为4的倍数即可检验真假;根据小仁的发现列式:y2-(y-2)2=2 016求解,根据所得解即可检验真假.
(1)若28都是“神秘数”,设28是由x和x-2两数的平方差得到的
则x2-(x-2)2=28,解得:x=8,
∴x-2=6,
即28=82-62,28是“神秘数”
(2)① (2k+2)2-(2k)2=(2k+2-2k)(2k+2+2k)=4(2k+1),
∴由2k+2和2k构造的“神秘数”是4的倍数,且是奇数倍
或②设2 016是由y和y-2两数的平方差得到的,
则y2-(y-2)2=2 016,
解得:y=505,不是偶数,
∴2 016不是“神秘数”.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,给出四个点阵,![]() 表示每个点阵中点的个数,按照图形中的点的个数变化规律,
表示每个点阵中点的个数,按照图形中的点的个数变化规律,
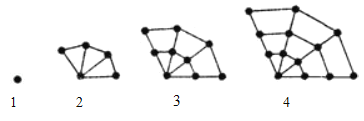
(1)请问第![]() 个点阵中的点的个数
个点阵中的点的个数![]() _________.
_________.
(2)猜想第![]() 个点阵中的点的个数
个点阵中的点的个数![]() ________.
________.
(3)若已知点阵中点的个数为![]() ,问这个点阵是第几个?
,问这个点阵是第几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018雾霾天气趋于严重,某商场根据民众健康需要,从厂家购进了A,B两种型号的空气净化器,如果销售15台A型和10台B型空气净化器的利润为6000元,销售10台A型和15台B型空气净化器的利润为6500元.
(1)求每台A型空气净化器和B型空气净化器的销售利润;
(2)该商场计划一次购进两种型号的空气净化器共160台,其中B型空气净化器的进货量不超过A型空气净化器的2倍,设购进A型空气净化器x台,这160台空气净化器的销售总利润为y元.
①求y关于x的函数关系式;
②该公司购进A型、B型空气净化器各多少台时,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=18,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )

A. 6![]() B. 7
B. 7![]() C. 8
C. 8![]() D. 9
D. 9![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
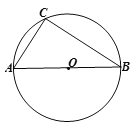
【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面中两条直线l1和l2相交于点O,对于平面上任意点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.根据上述定义,有以下几个结论:①“距离坐标”是(0,2)的点有1个;②“距离坐标”是(3,4)的点有4个;③“距离坐标”(p,q)满足p=q的点有4个.其中正确的有( )
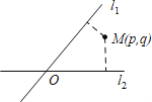
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:
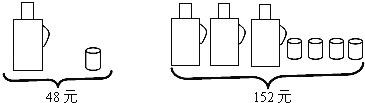
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com