练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

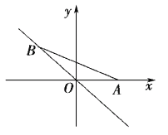
    【题目】如图，点A的坐标为（1，0），点B在直线y=-x上运动，当线段AB最短时，点B的坐标为____.

    【答案】（，）．

    【解析】

    线段AB最短，说明AB此时为点A到y=﹣x的距离．过A点作垂直于直线y=﹣x的垂线AB，由题意可知：△AOB为等腰直角三角形，过B作BC垂直x轴垂足为C，则点C为OA的中点，有OC=BC，故可确定出点B的坐标．

    过A点作垂直于直线y=﹣x的垂线AB．

    ∵点B在直线y=﹣x上运动，∴∠AOB=45°，∴△AOB为等腰直角三角形，过B作BC垂直x轴垂足为C，则点C为OA的中点，则OC=BC．

    作图可知B在x轴下方，y轴的右方，∴横坐标为正，纵坐标为负．

    所以当线段AB最短时，点B的坐标为（，）．

    故答案为：（，）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

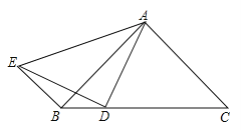
    【题目】如图，在△ABC中，AB=AC，D是BC边上一点，连接AD，E为△ABC外一点，连接DE，AE和BE，AD=DE，BE∥AC.求证：∠BED=∠DAB.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

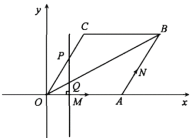
    【题目】如图，在直角坐标系XOY中，菱形OABC的边OA在x轴正半轴上，点B，C在第一象限，∠C=120°，边长OA=8，点M从原点O出发沿x轴正半轴以每秒1个单位长的速度作匀速运动，点N从A出发沿边AB—BC—CO以每秒2个单位长的速度作匀速运动.过点M作直线MP垂直于x轴并交折线OCB于P，交对角线OB于Q，点M和点N同时出发，分别沿各自路线运动，点N运动到原点O时，M和N两点同时停止运动.

    （1）当t=2时，求线段PQ的长；

    （2）求t为何值时，点P与N重合；

    （3）设△APN的面积为S，求S与t的函数关系式及t的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．

    （1）求证：AE与⊙O相切于点A；

    （2）若AE∥BC，BC=2，AC=2，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲骑自行车从M地出发沿一条公路匀速前往N地，乙骑摩托车从N地出发沿同一条公路匀速前往M地，

    已知乙比甲晚出发0.5小时且先到达目的地．设甲行驶的时间为t(h)，甲乙两人之间的路程为y(km)，

    y与t的函数关系如图1所示，请解决以下问题：

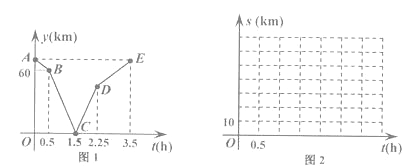
    （1）写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式．

    （2）①求点D的纵坐标．

    ②求M，N两地之间的距离．

    （3）设乙离M地的路程为S乙 (km)，请直接写出S甲 与时间t(h)的函数表达式，并在图2所给的直角坐标系中画出它的图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如：4＝22－02，12＝42－22，20＝62－42，因此4，12，20都是“神秘数”.

    （1）试分析28是否为“神秘数”；

    （2）下面是两个同学演算后的发现，请选择一个“发现”，判断真、假，并说明理由．

    ①小能发现：两个连续偶数2k＋2和2k(其中k取非负整数)构造的“神秘数”也是4的倍数．

    ②小仁发现：2016是“神秘数”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．

    （1）该商场两次共购进这种运动服多少套？

    （2）如果这两批运动服每套的售价相同，且全部售完后总利润不低于20%，那么每套售价至少是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，一次函数y=－2x与二次函数y＝ax2＋2ax＋c的图像交于A、B两点(点A在点B的右侧)，与其对称轴交于点C．

    （1）求点C的坐标；

    （2）设二次函数图像的顶点为D，点C与点D关于 x轴对称，且△ACD的面积等于2.

    ① 求二次函数的解析式；

    ② 在该二次函数图像的对称轴上求一点P（写出其坐标），使△PBC与△ACD相似.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践：某“综合与实践”小组开展了“正方体纸盒的制作”实践活动，他们利用长为，宽为长方形纸板制作出两种不同方案的正方体盒子， 请你动手操作验证并完成任务．(纸板厚度及接缝处忽略不计)

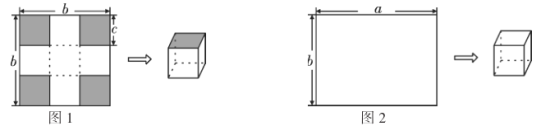
    动手操作一：

    如图1，若，按如图1所示的方式先在纸板四角剪去四个同样大小边长为的小正方形，再沿虚线折合起来就可以做成一个无盖的正方体纸盒．

    问题解决：（1）此时，你发现与之间存在的数量关系为 ．

    动手操作二：

    如图2，若，现在在纸板的四角剪去两个小正方形和两个小长方形恰好可以制作成一个有盖的正方体纸盒，其大小与（1）中无盖正方体大小一样．

    拓展延伸：（2）请你在图2中画出你剪去的两个小正方形和两个小长方形(用阴影表示)，折痕用虚线表示；

    （3）此时，你发现与之间存在的数量关系为 ；若，求有盖正方体纸盒的表面积．

    查看答案和解析>>

    同步练习册答案