
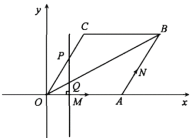
����Ŀ����ͼ����ֱ������ϵXOY�У�����OABC�ı�OA��x���������ϣ���B��C�ڵ�һ���ޣ���C=120�����߳�OA=8����M��ԭ��O������x����������ÿ��1����λ�����ٶ��������˶�����N��A�����ر�AB��BC��CO��ÿ��2����λ�����ٶ��������˶�.����M��ֱ��MP��ֱ��x�Ტ������OCB��P�����Խ���OB��Q����M�͵�Nͬʱ�������ֱ��ظ���·���˶�����N�˶���ԭ��Oʱ��M��N����ͬʱֹͣ�˶�.
��1����t=2ʱ�����߶�PQ�ij���
��2����tΪ��ֵʱ����P��N�غϣ�
��3�����APN�����ΪS����S��t�ĺ�����ϵʽ��t��ȡֵ��Χ.
���𰸡���1��PQ=![]() ����2��t=
����2��t=![]() ��ʱ����P��N�غ�����3��S��t�ĺ�����ϵʽΪ��
��ʱ����P��N�غ�����3��S��t�ĺ�����ϵʽΪ��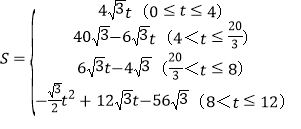 .
.
����������1����ֱ�����������PM��QM���ɽ�����⣻
��2�����ݵ�P��N��·��֮��=24���������̼��ɽ��������
��3�����������ο������⼴�ɽ������.
��1��������OABC����AOC=60������AOQ=30����
��t=2ʱ��OM=2��PM=2![]() ��QM=
��QM=![]() ��PQ=
��PQ=![]() .
.
��2����t��4ʱ��AN=PO=2OM=2t��
t=4ʱ��P����C�㣬N����B�㣬��P��N�ڱ�BC������.
��t��ʱ����P��N�غϣ���(t-4)+2(t-4)=8,
��t=![]() .
.
��t=![]() ��ʱ����P��N�غ�.
��ʱ����P��N�غ�.
��3���ٵ�0��t��4ʱ��PN=OA=8����PN��OA��PM=![]() t��
t��
S��APN=![]() ��8��
��8��![]() t=4
t=4![]() t��
t��
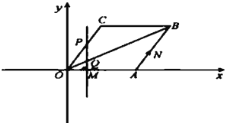
�ڵ�4��t��![]() ʱ��PN=8-3(t-4)=20-3t��
ʱ��PN=8-3(t-4)=20-3t��
S��APN=![]() ��4
��4![]() ��(20-3t)=40
��(20-3t)=40![]() -6
-6![]() t��
t��
�۵�![]() ��t��8ʱ��PN=3(t-4)-8=3t-20��
��t��8ʱ��PN=3(t-4)-8=3t-20��
S��APN=![]() ��4
��4![]() ��(3t-20)= 6
��(3t-20)= 6![]() t -4
t -4![]() ��
��
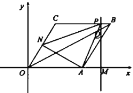
��8��t��12ʱ��ON=24-2t��N��OM����Ϊ12![]() -
-![]() t,
t,
N��CP����Ϊ4![]() -(12
-(12![]() -
-![]() t)=
t)= ![]() t-8
t-8![]() ��CP=t-4��BP=12-t��
��CP=t-4��BP=12-t��
S��APN=S����-S��AON- S��CPN- S��APB
=32![]() -
-![]() ��8��(12
��8��(12![]() -
-![]() t)-
t)- ![]() ��t-4����
��t-4����![]() t-8
t-8![]() ��-
��-![]() ��12-t����4
��12-t����4![]()
= - ![]() t2+12
t2+12![]() t-56
t-56![]()
���ϣ�S��t�ĺ�����ϵʽΪ��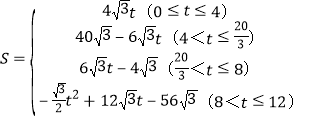



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
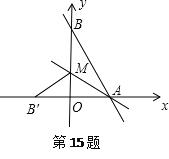
����Ŀ����ͼ��ֱ��y=��![]() x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦����ֱ��AM�Ľ���ʽΪ �� ��
x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦����ֱ��AM�Ľ���ʽΪ �� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��������߶ν�һ�������ηֳ�3��С���������Σ����ǰ��������߶ν�����������ε������ߣ�����ABC�У���B��30�㣬AD�� DE����ABC�������ߣ���D�� BC ���ϣ���E�� AC���ϣ���AD��BD��DE��CE����д����C���п��ܵĶ���________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l:y=kx+1��������y=x2-4x
��1����֤��ֱ��l��������������������㣻
��2����ֱ��l���������������ΪA��B��OΪԭ�㣬��k=-2ʱ�����OAB�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧϰ��ʽʱ���֣����������ʹ�ó˷���ʽ���Լ����㣬�����ڽ�˵�������ʱ�����������ģ����£���
![]()
![]() ��һ��
��һ��
![]() �ڶ���
�ڶ���
С������С������������˵�����������ˣ��ڵ�һ�����ù�ʽʱ�����˴�����úü��һ�£���С��������ϸ�����Լ�������һ������Ȧ���˳������������˾��������£���
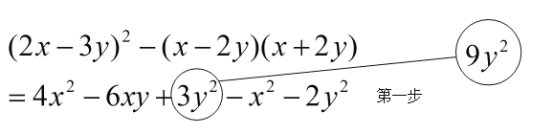
С������С���ĸĴ���˵�����㻹�д�û�иij�������
��1������ΪС��˵�Ķ���_________������������������������
��2�����С��˵�Ķԣ���ôС��������Щ����û���ҳ������������С���ѵ�һ���е���������Ȧ��������������Ȼ��д���������ȷ������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018���������������أ�ij�̳��������ڽ�����Ҫ���ӳ��ҹ�����A��B�����ͺŵĿ������������������15̨A�ͺ�10̨B�Ϳ���������������Ϊ6000Ԫ������10̨A�ͺ�15̨B�Ϳ���������������Ϊ6500Ԫ��
��1����ÿ̨A�Ϳ�����������B�Ϳ�������������������
��2�����̳��ƻ�һ�ι��������ͺŵĿ�����������160̨������B�Ϳ����������Ľ�����������A�Ϳ�����������2�����蹺��A�Ϳ���������x̨����160̨����������������������ΪyԪ��
����y����x�ĺ�����ϵʽ��
�ڸù�˾����A�͡�B�Ϳ���������������̨ʱ������ʹ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ʵ��ڵ�һ����x�ᡢy�����˶����ڵ�һ���ӣ�����ԭ���˶�����0��1����Ȼ����Ű�ͼ�м�ͷ��ʾ�����˶�{����0��0������0��1������1��1������1��0����}����ÿ���ƶ�һ����λ����ô��35��ʱ�ʵ�����λ�õ������ǣ�������
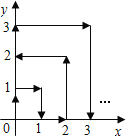
A. ��4��0��B. ��5��0��C. ��0��5��D. ��5��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A������Ϊ��1��0������B��ֱ��y=-x���˶������߶�AB���ʱ����B������Ϊ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ��Ϊ�˽��Уѧ��ϲ������������������ȡ��������ѧ�������ʾ����飨Ҫ��ÿλѧ��ֻ����дһ���Լ�ϲ�������ࣩ���������˵Ľ�����Ƴ����µ�������������ͳ��ͼ��
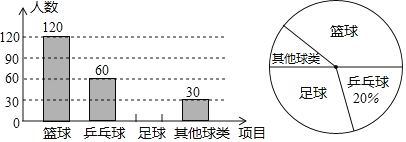
�����ͼ���ṩ����Ϣ��������������
��1���μӵ��˵�ѧ�������� ���ˣ�������ͼ�У���ʾ���������ࡱ������Բ�Ľ�Ϊ�� ���ȣ�
��2��������ͼ����������
��3������У��2300��ѧ���������ϲ��������ѧ�������� ���ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com