
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
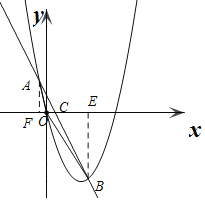
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】(1)联立两解析式,根据判别式即可求证;
(2)画出图象,求出A、B的坐标,再求出直线y=-2x+1与x轴的交点C,然后利用三角形的面积公式即可求出答案.
(1)联立![]()
化简可得:x2-(4+k)x-1=0,
∴△=(4+k)2+4>0,
故直线l与该抛物线总有两个交点;
(2)当k=-2时,
∴y=-2x+1
过点A作AF⊥x轴于F,过点B作BE⊥x轴于E,
∴联立![]()
解得:![]() 或
或![]()
∴A(1-![]() ,2
,2![]() -1),B(1+
-1),B(1+![]() ,-1-2
,-1-2![]() )
)
∴AF=2![]() -1,BE=1+2
-1,BE=1+2![]()
易求得:直线y=-2x+1与x轴的交点C为(![]() ,0)
,0)
∴OC=1
∴S△AOB=S△AOC+S△BOC
=![]() OCAF+
OCAF+![]() OCBE
OCBE
=![]() OC(AF+BE)
OC(AF+BE)
=![]() ×(2
×(2![]() -1+1+2
-1+1+2![]() )
)
=2![]() .
.


科目:初中数学 来源: 题型:
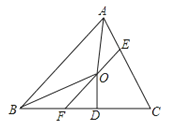
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列三个结论: ①∠AOB=90°+![]() ;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )
;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )
A. ①②③B. ①③C. ①②D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
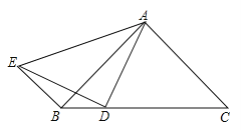
【题目】如图,在△ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;

(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
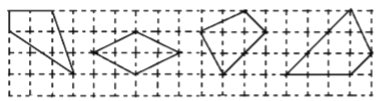
【题目】如图所示,网格线是由边长为1的小正方形格子组成的,小正方形的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.小明与数学小组的同学研究发现,内部含有3个格点的四边形的面积与该四边形边上的格点数有某种关系,请你观察图中的4个格点四边形.设内部含有3个格点的四边形的面积为![]() ,其各边上格点的个数之和为
,其各边上格点的个数之和为![]() ,则
,则![]() 与
与![]() 之间的关系式为__________.
之间的关系式为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
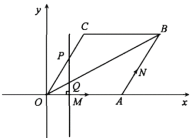
【题目】如图,在直角坐标系XOY中,菱形OABC的边OA在x轴正半轴上,点B,C在第一象限,∠C=120°,边长OA=8,点M从原点O出发沿x轴正半轴以每秒1个单位长的速度作匀速运动,点N从A出发沿边AB—BC—CO以每秒2个单位长的速度作匀速运动.过点M作直线MP垂直于x轴并交折线OCB于P,交对角线OB于Q,点M和点N同时出发,分别沿各自路线运动,点N运动到原点O时,M和N两点同时停止运动.
(1)当t=2时,求线段PQ的长;
(2)求t为何值时,点P与N重合;
(3)设△APN的面积为S,求S与t的函数关系式及t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=-2x与二次函数y=ax2+2ax+c的图像交于A、B两点(点A在点B的右侧),与其对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D,点C与点D关于 x轴对称,且△ACD的面积等于2.
① 求二次函数的解析式;
② 在该二次函数图像的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com