
【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;

(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

【答案】(1)角平分线上的点到角的两边距离相等;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据角平分线的性质定理解答;
(2)作DE⊥BA交BA延长线于E,DF⊥BC于F,证明△DEA≌△DFC,根据全等三角形的性质证明;
(3)在BC时截取BK=BD,连接DK,根据(2)的结论得到AD=DK,根据等腰三角形的判定定理得到KD=KC,结合图形证明.
(1)∵BD平分∠ABC,∠BAD=90°,∠BCD=90°,∴DA=DC(角平分线上的点到角的两边距离相等).
故答案为:角平分线上的点到角的两边距离相等;
(2)如图2,作DE⊥BA交BA延长线于E,DF⊥BC于F.
∵BD平分∠EBF,DE⊥BE,DF⊥BF,∴DE=DF.
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,∴∠EAD=∠C.
在△DEA和△DFC中,∵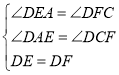 ,∴△DEA≌△DFC(AAS),∴DA=DC;
,∴△DEA≌△DFC(AAS),∴DA=DC;
(3)如图,在BC时截取BK=BD,连接DK.
∵AB=AC,∠A=100°,∴∠ABC=∠C=40°.
∵BD平分∠ABC,∴∠DBK![]() ∠ABC=20°.
∠ABC=20°.
∵BD=BK,∴∠BKD=∠BDK=80°,即∠A+∠BKD=180°,由(2)的结论得AD=DK.
∵∠BKD=∠C+∠KDC,∴∠KDC=∠C=40°,∴DK=CK,∴AD=DK=CK,∴BD+AD=BK+CK=BC.



 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
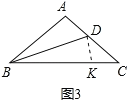
【题目】(1)阅读理解:如图1,在![]() 中,若
中,若![]() ,
,![]() .求
.求![]() 边上的中线
边上的中线![]() 的取值范围.小聪同学是这样思考的:延长
的取值范围.小聪同学是这样思考的:延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() .利用全等将边
.利用全等将边![]() 转化到
转化到![]() ,在
,在![]() 中利用三角形三边关系即可求出中线
中利用三角形三边关系即可求出中线![]() 的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线
的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线![]() 的取值范围是__________.
的取值范围是__________.
(2)问题解决:如图2,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,若
边上,若![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,且BA=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亚奥理事会于![]() 年
年![]() 月3
月3![]() 日在土库曼斯坦阿什哈巴德举行第
日在土库曼斯坦阿什哈巴德举行第![]() 届代表大会,并在会上投票选出
届代表大会,并在会上投票选出![]() 年第
年第![]() 届亚运会举办城市为杭州.
届亚运会举办城市为杭州.![]() 个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间
个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间![]() 年
年![]() 月
月![]() 日
日![]() 时应是( ).
时应是( ).

A.伦敦时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
B.巴黎时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
C.智利时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
D.曼谷时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形 ABC (顶点是网格线交点的三角形)的顶点 A ,C 的坐标分别是(-4 ,6) ,(-1,4) .
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC 关于 x 轴对称的△A1B1C1 ;并直接写出A1B1C1的坐标.
(3)请在 y 轴上求作一点 P ,使△PB1C 的周长最小,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )

A. (3,-1) B. (-1,-1) C. (1,1) D. (-2,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
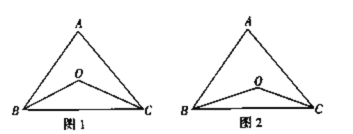
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )
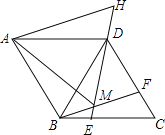
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com