
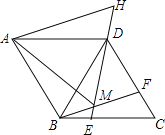
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题分析:∵四边形ABCD是菱形, AB=BD,∴AB=BD=AD,∴△ABD是等边三角形,
∴∠BDF=∠C=60°,又∵BE=CF,∴BC﹣BE=CD﹣CF,即CE=DF,
在△BDF和△DCE中,  ,
,
∴△BDF≌△DCE(SAS),故①小题正确;
∴∠DBF=∠EDC,
∵∠DMF=∠DBF+∠BDE=∠EDC+∠BDE=∠BDC=60°,
∴∠BMD=180°﹣∠DMF=180°﹣60°=120°,故②小题正确;
∵∠DEB=∠EDC+∠C=∠EDC+60°,∠ABM=∠ABD+∠DBF=∠DBF+60°,
∴∠DEB=∠ABM,
又∵AD∥BC,∴∠ADH=∠DEB,∴∠ADH=∠ABM,
在△ABM和△ADH中, 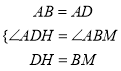 ,
,
∴△ABM≌△ADH(SAS),
∴AH=AM,∠BAM=∠DAH,
∴∠MAH=∠MAD+∠DAH=∠MAD+∠BAM=∠BAD=60°,
∴△AMH是等边三角形,故③小题正确;
∵△ABM≌△ADH,
∴△AMH的面积等于四边形ABMD的面积,
又∵△AMH的面积=![]() AM
AM![]() AM=
AM=![]() AM2,
AM2,
∴S四边形ABMD=![]() AM2,
AM2,
S四边形ABCD≠S四边形ABMD,故④小题错误,
综上所述,正确的是①②③共3个.
故选:C.


科目:初中数学 来源: 题型:
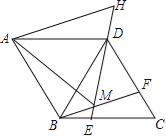
【题目】如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;

(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:□ABCD的两边AB,AD的长是关于x的方程x2-mx+![]() -
-![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2014年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |

(1)表中的a=________,b=________;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图①,我们把一个四边形![]() 的四边中点
的四边中点![]() 依次连接起来得到的四边形
依次连接起来得到的四边形![]() 是平行四边形吗?
是平行四边形吗?
小敏在思考问题,有如下思路:连接![]() .
.

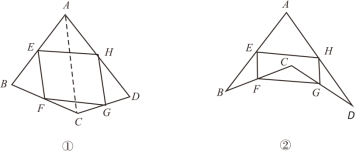
结合小敏的思路作答.
(1)若只改变图①中四边形![]() 的形状(如图②),则四边形
的形状(如图②),则四边形![]() 还是平行四边形吗?说明理由;
还是平行四边形吗?说明理由;
(参考小敏思考问题方法)
(2)如图②,在(1)的条件下,若连接![]() .
.
①当![]() 与
与![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形,写出结论并证明;
是矩形,写出结论并证明;
②当![]() 与
与![]() 满足____时,四边形
满足____时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com