
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图①,我们把一个四边形![]() 的四边中点
的四边中点![]() 依次连接起来得到的四边形
依次连接起来得到的四边形![]() 是平行四边形吗?
是平行四边形吗?
小敏在思考问题,有如下思路:连接![]() .
.

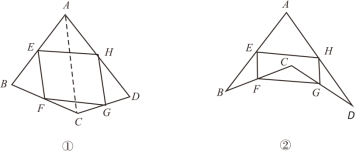
结合小敏的思路作答.
(1)若只改变图①中四边形![]() 的形状(如图②),则四边形
的形状(如图②),则四边形![]() 还是平行四边形吗?说明理由;
还是平行四边形吗?说明理由;
(参考小敏思考问题方法)
(2)如图②,在(1)的条件下,若连接![]() .
.
①当![]() 与
与![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形,写出结论并证明;
是矩形,写出结论并证明;
②当![]() 与
与![]() 满足____时,四边形
满足____时,四边形![]() 是正方形.
是正方形.
【答案】(1)是,理由见解析;(2)①AC⊥BD,证明见解析;②AC⊥BD且AC=BD
【解析】
(1)连接AC,根据三角形中位线的性质得到EF∥AC,EF=![]() AC,然后根据平行四边形判定定理即可得到结论;
AC,然后根据平行四边形判定定理即可得到结论;
(2)①根据平行线的性质得到GH⊥BD,GH⊥GF,于是得到∠HGF=90°,根据矩形的判定定理即可得到结论;
②在①基础上,只要证明∠EHG=90°即可;
解:(1)四边形EFGH是平行四边形,理由如下:
如图2,连接AC,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,EF=![]() AC,
AC,
同理HG∥AC,HG=![]() AC,
AC,
综上可得:EF∥HG,EF=HG,
故四边形EFGH是平行四边形;
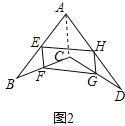
(2)①当AC⊥BD时,四边形EFGH为矩形;
理由如下:
同(1)得:四边形EFGH是平行四边形,
∵AC⊥BD,GH∥AC,
∴GH⊥BD,
∵GF∥BD,
∴GH⊥GF,
∴∠HGF=90°,
∴四边形EFGH为矩形;

②结论:当AC⊥BD且AC=BD时,四边形EFGH是正方形.
理由:由①可知,AC=BD,四边形EFGH是菱形,
∵AC⊥BD,AC∥HG,
∴HG⊥BD,
∵EH∥BD,
∴EH⊥HG,
∴∠EHG=90°,
∴四边形EFGH是正方形.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,且BA=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
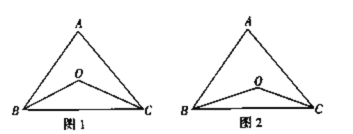
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
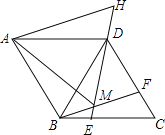
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是□ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
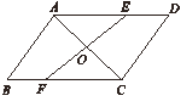
(1)求证:△AOE≌△COF;
(2)若EF与AC垂直,试判断四边形AFCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AB=6,AC=8,D 为 AC 上一点,将△ABD 沿 BD 折叠,使点 A 恰好落在 BC 上的 E 处,则折痕 BD 的长是( )

A.5B.![]() C.3
C.3 ![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com