
【题目】如图,AC是□ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
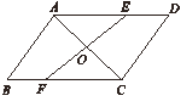
(1)求证:△AOE≌△COF;
(2)若EF与AC垂直,试判断四边形AFCE的形状,并说明理由.
【答案】(1)详见解析;(2)四边形AFCE是菱形,理由详见解析.
【解析】
(1)由平行四边形的性质得出AD∥BC,得出∠EAO=∠FCO,利用对顶角相等∠AOE=∠COF,O是AC的中点,OA=OC,所以由ASA即可得出结论;(2)四边形AFCE是菱形,先证明四边形AFCE是平行四边形,再由对角线互相垂直的平行四边形是菱形即可得出四边形AFCE是菱形.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵O是CA的中点
∴OA=OC,
又∵∠AOE=∠COF(对顶角相等),
∴△AOE≌△COF(ASA);
(2)四边形AFCE是菱形,理由如下:
∵△AOE≌△COF,
∴AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵EF⊥AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).


科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
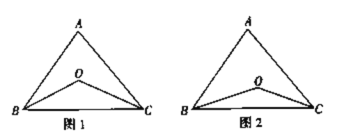
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:□ABCD的两边AB,AD的长是关于x的方程x2-mx+![]() -
-![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射手在同一条件下进行射击,结果如下表所示:

(1)计算并填写表中击中靶心的频率;(结果保留三位小数)
(2)这个射手射击一次,击中靶心的概率估计值是多少?(结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图①,我们把一个四边形![]() 的四边中点
的四边中点![]() 依次连接起来得到的四边形
依次连接起来得到的四边形![]() 是平行四边形吗?
是平行四边形吗?
小敏在思考问题,有如下思路:连接![]() .
.

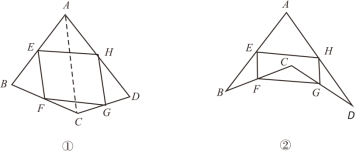
结合小敏的思路作答.
(1)若只改变图①中四边形![]() 的形状(如图②),则四边形
的形状(如图②),则四边形![]() 还是平行四边形吗?说明理由;
还是平行四边形吗?说明理由;
(参考小敏思考问题方法)
(2)如图②,在(1)的条件下,若连接![]() .
.
①当![]() 与
与![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是矩形,写出结论并证明;
是矩形,写出结论并证明;
②当![]() 与
与![]() 满足____时,四边形
满足____时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1500名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 人数 |
乒乓球 | 42 |
羽毛球 | a |
排球 | 15 |
篮球 | 33 |
足球 | b |
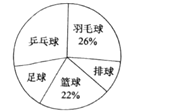
![]()
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,a=________,b=________;
(3)试估计上述1500名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF,
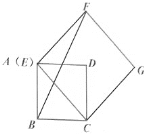
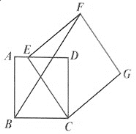
图1 图2
(1)如图1,当点E与点A重合时,则![]() _____;
_____;
(2)如图2,当点E在线段AD上时,![]() ,
,
①求点F到AD的距离;
②求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com