
����Ŀ��ѧУ��ͼ�����ͬһ����ֱ��·�ϣ��״�ѧУȥͼ��ݣ��Ҵ�ͼ��ݻ�ѧУ���ס������˶����ٲ�����ͬʱ���������ȵ���Ŀ�ĵأ�����֮��ľ���y���ף���ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ��

��1������ͼ����Ϣ����t���� ������ʱ�����������������ٶ�Ϊ�� ����/���ӣ��ҵ��ٶ�Ϊ�� ����/���ӣ�
��2��ͼ�е�A������Ϊ�� ����
��3�����߶�AB��ֱ�ߵĺ�������ʽ��
��4�������������У���ʱ�������400�ף�
���𰸡���1��24��40��60����2����40��1600������3���߶�AB����ʾ�ĺ�������ʽΪy��40x����4�������������У���20���Ӻ�28����ʱ�������400��
��������
��1������ͼ����Ϣ����![]() ����ʱ����������������60������ʻ2400�ף������ٶ�
����ʱ����������������60������ʻ2400�ף������ٶ�![]() ·��
·��![]() ʱ��ɵü��ٶȣ���������ҵ��ٶȣ�
ʱ��ɵü��ٶȣ���������ҵ��ٶȣ�
��2������Ҵ�ͼ��ݻ�ѧУ��ʱ�伴![]() ��ĺ����ꣻ
��ĺ����ꣻ
��3�����ô���ϵ������⼴�ɣ�
��4��������ǰ�����������ɣ�
�⣺��1������ͼ����Ϣ����t��24����ʱ�����������������ٶ�Ϊ2400��60��40����/���ӣ���
���ס������˵��ٶȺ�Ϊ2400��24��100��/���ӣ�
���ҵ��ٶ�Ϊ100��40��60����/���ӣ���
�ʴ�Ϊ��24��40��60��
��2���Ҵ�ͼ��ݻ�ѧУ��ʱ��Ϊ2400��60��40�����ӣ���
40��40��1600��
��A���������40��1600����
�ʴ�Ϊ����40��1600����
��3�����߶�AB����ʾ�ĺ�������ʽΪy��kx+b��
��A��40��1600����B��60��2400����
��![]() �����
�����![]() ��
��
���߶�AB����ʾ�ĺ�������ʽΪy��40x��
��4�������������ӭ�棺��2400��400����100��20�����ӣ���
���߹�����2400+400����100��28�����ӣ���
�������������У���20���Ӻ�28����ʱ�������400�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�������������У�ÿһ��С�����εı߳�Ϊ1.��������� ABC (�����������߽����������)�Ķ��� A ��C ������ֱ���(-4 ��6) ��(-1��4) ��
(1)����ͼ�е�����ƽ���ڽ���ƽ��ֱ������ϵ��
(2)�뻭����ABC ���� x ��ԳƵ���A1B1C1 ����ֱ��д��A1B1C1������.
(3)���� y ��������һ�� P ��ʹ��PB1C ���ܳ���С��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC����ABCD��һ���Խ��ߣ���AC�е�O��ֱ�߷ֱ�AD��BC�ڵ�E��F��
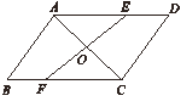
��1����֤����AOE�ա�COF��
��2����EF��AC��ֱ�����ж��ı���AFCE����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ABCD�У�E��CD����һ�㣬
��1������ADE�Ƶ�A��˳ʱ�뷽����ת��ʹAD��AB�غϣ��õ���ABF����ͼ1��ʾ���۲��֪����DE��ȵ��߶����� ������AFB=���� ��
��2����ͼ2��������ABCD�У�P��Q�ֱ���BC��CD���ϵĵ㣬�ҡ�PAQ=45������ͨ����ת�ķ�ʽ˵����DQ+BP=PQ��
��3���ڣ�2�����У�����BD�ֱ�AP��AQ��M��N���㻹������ת��˼��˵��BM2+DN2=MN2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ڽ�����O������A��ֱ��EF��

��1����ͼ����ʾ����ABΪ��O��ֱ����ҪʹEF��Ϊ��O�����ߣ�����Ҫ���ӵ�һ�������ǣ�����˵�����֣��� ���� ��
��2����ͼ����ʾ�����AB�Dz���Բ��O���ң�����CAE=��B����ôEF����O����������֤������жϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]() ��
��
��1�����˷��̵�һ����Ϊ1����![]() ��ֵ��
��ֵ��
��2����֤������![]() ȡ��ʵ�����˷��̶�����������ȵ�ʵ������
ȡ��ʵ�����˷��̶�����������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⣺����ֱ��������ABC�У���֪���߳�Ϊ3��4��������߳�Ϊ5���������ε�����a��b��c����a2+c2��b2�����C��90�����ۡ�ABC�У�����A����B����C��1��5��6�����ABC��ֱ�������Σ��ܡ�ABC�У���a��b��c��1��2��![]() ���������������ֱ�������Σ����У���ȷ����Ϊ_____��ѡ����ţ���
���������������ֱ�������Σ����У���ȷ����Ϊ_____��ѡ����ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��5��31�գ���ƽ���ٰ���������꼶ѧ������ѧ���Ļ��Ķ�չʾ�����Ϊ�����ڱ��λ�б��������ѧ������ʦ������6��1�չ���ʴ����ɫǦ����Ϊ��Ʒ. ��֪1���ʴ���2Ͳ��ɫǦ��ԭ�۹���44Ԫ��2���ʴ���3Ͳ��ɫǦ��ԭ�۹���73Ԫ.
��1��ÿ���ʴ���ÿͲ��ɫǦ��ԭ�۸�����Ԫ��
��2��ʱ�ꡰ��ͯ�ڡ����̵���С��Żݴ������������취���£��ʴ������ۡ��Żݣ���ɫǦ�ʲ�����10Ͳ���Żݣ�����10Ͳ�IJ��֡����ۡ��Ż�. ����x���ʴ���Ҫy1Ԫ����xͲ��ɫǦ����Ҫy2Ԫ. ���ú�x�Ĵ���ʽ��ʾy1��y2��
��3�����ڣ�2���������¹���ͬһ�ֽ�Ʒ95����������������ֽ�ƷʡǮ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У�BE ƽ�֡�ABC��DE��BC.
��1���жϡ�DBE ��ʲô�����Σ���˵�����ɣ�
��2���� F Ϊ BE �е㣬��ABC��58�㣬��˵�� DF��BE�������EDF �Ķ�����
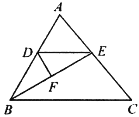
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com