练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】给出下列命题：①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；②三角形的三边a、b、c满足a2+c2＝b2，则∠C＝90°；③△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC是直角三角形；④△ABC中，若a：b：c＝1：2：，则这个三角形是直角三角形，其中，正确命题为_____（选填序号）．

    【答案】③④

    【解析】

    根据勾股定理、三角形内角和定理、勾股定理的逆定理判断．

    解：①在直角三角形中，已知两边长为3和4，

    当4是直角边时，第三边，

    当4是斜边长时，第三边

    则第三边长为5或，本说法是假命题；

    ②三角形的三边、、满足，则，本说法是假命题；

    ③中，若，

    设、、分别为、、，

    则，

    解得，，

    则、、分别为、、，

    则是直角三角形，本说法是真命题；

    ④中，若，

    设、、分别为、、，

    ，，

    ，

    这个三角形是直角三角形，本说法是真命题，

    故答案为：③④．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

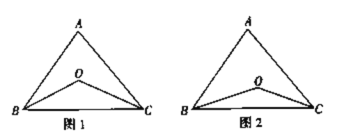
    【题目】已知任意一个三角形的三个内角的和是180°，如图1，在ABC中，∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.

    （1）若∠A=70°，求∠BOC的度数；

    （2）若∠A=α，求∠BOC的度数；

    （3）如图2，若BO、CO分别是∠ABC、∠ACB的三等分线，也就是∠OBC=∠ABC，∠OCB=∠ACB，∠A=α，求∠BOC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

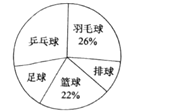
    【题目】某中学为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1500名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：

    球类名称

    人数

    乒乓球

    42

    羽毛球

    a

    排球

    15

    篮球

    33

    足球

    b

    解答下列问题：

    （1）这次抽样调查中的样本是________；

    （2）统计表中，a=________，b=________；

    （3）试估计上述1500名学生中最喜欢乒乓球运动的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．

    （1）根据图象信息，当t＝　 　分钟时甲乙两人相遇，甲的速度为　 　米/分钟，乙的速度为　 　米/分钟；

    （2）图中点A的坐标为　 　；

    （3）求线段AB所直线的函数表达式；

    （4）在整个过程中，何时两人相距400米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

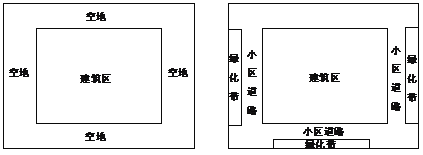
    【题目】如左图,某小区的平面图是一个400×300平方米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%,并且南北空地与东西空地的宽度各自相同.

    （1）求该小区南北空地的宽度；

    （2）如右图,该小区在东西南三块空地上做如图所示的矩形绿化带,绿化带与建筑区之间为小区道路,小区道路宽度一致.已知东西侧绿化带完全相同,其长约为200米,南侧绿化带的长为300米,绿化面积为18000平方米,请求出小区道路的宽度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.

    （1）求证：OE是CD的垂直平分线.

    （2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一项工程甲队单独完成所需天数是乙队单独完成这项工程所需天数的；若由乙队先做45天，剩下的工程再由甲、乙两队合作54天可以完成。

    （1）求甲、乙两队单独完成这项工程各需要多少天？

    （2）已知甲队每天的施工费用为0.82万元，乙队每天的施工费用为0.68万元，工程预算的施工费用为100万元.拟安排甲、乙两队同时合作完成这项工程，则工程预算的施工费用是否够用？若不够用，需追加预算多少万元？说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD是边长为4的正方形，点E在边AD所在的直线上，连接CE，以CE为边，作正方形CEFG(点D，点F在直线CE的同侧)，连接BF，

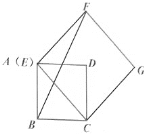
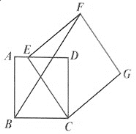
    图1 图2

    (1)如图1，当点E与点A重合时，则_____；

    (2)如图2，当点E在线段AD上时，，

    ①求点F到AD的距离；

    ②求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校八年级有800名学生，在一次跳绳模拟测试中，从中随机抽取部分学生，根据其测试成绩制作了下面两个统计图，请根据相关信息，解答下列问题：

    （1）本次抽取到的学生人数为______，扇形统计图中的值为______．

    （2）本次调查获取的样本数据的众数是_____（分），中位数是_____（分）．

    （3）根据样本数据，估计我校八年级模拟体测中得12分的学生约有多少人？

    查看答案和解析>>

    同步练习册答案