
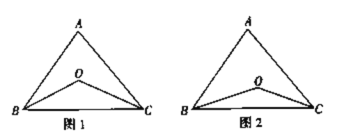
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
【答案】(1)125°;(2)90°+![]() ;(3)120°+
;(3)120°+![]()
【解析】
(1)根据三角形的内角和定理求出∠ABC+∠ACB,根据角平分线的定义求出∠OBC+∠OCB,根据三角形内角和定理求出即可;
(2)根据三角形的内角和定理求出∠ABC+∠ACB,根据角平分线的定义求出∠OBC+∠OCB,根据三角形内角和定理求出即可;
(3)根据三角形的内角和定理求出∠ABC+∠ACB,求出∠OBC+∠OCB,根据三角形内角和定理求出即可.
(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°,
∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=55°,
(∠ABC+∠ACB)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=125°;
(2)∵∠A=α,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-α)=90°-
(180°-α)=90°-![]() α,
α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-![]() α)=90°+
α)=90°+![]() α;
α;
(3)∵∠A=α,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-α)=60°-
(180°-α)=60°-![]() α,
α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(60°-![]() α)=120°+
α)=120°+![]() α.
α.


科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接CE、DE、AC,CE与AD交于点F.

(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B.求证:四边形ACDE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形 ABC (顶点是网格线交点的三角形)的顶点 A ,C 的坐标分别是(-4 ,6) ,(-1,4) .
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC 关于 x 轴对称的△A1B1C1 ;并直接写出A1B1C1的坐标.
(3)请在 y 轴上求作一点 P ,使△PB1C 的周长最小,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
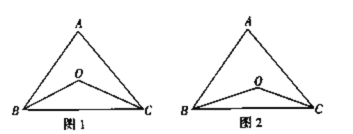
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月底统计知三月份的销量达到了500件.
(1)求二、三月份服装销售量的平均月增长率;
(2)从四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是□ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
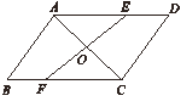
(1)求证:△AOE≌△COF;
(2)若EF与AC垂直,试判断四边形AFCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;④△ABC中,若a:b:c=1:2:![]() ,则这个三角形是直角三角形,其中,正确命题为_____(选填序号).
,则这个三角形是直角三角形,其中,正确命题为_____(选填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com