
ЁОЬтФПЁПФГЩЬГЁдкШЅФъЕзвдУПМў80дЊЕФНјМлЙКНјвЛХњЭЌаЭКХЕФЗўзАЃЌвЛдТЗнвдУПМў150дЊЕФЪлМлЯњЪлСЫ320МўЃЌЖўЁЂШ§дТЗнИУЗўзАГЉЯњЃЌЯњСПГжајзпИпЃЌдкЪлМлВЛБфЕФЧщПіЯТЃЌШ§дТЕзЭГМЦжЊШ§дТЗнЕФЯњСПДяЕНСЫ500МўЃЎ
ЃЈ1ЃЉЧѓЖўЁЂШ§дТЗнЗўзАЯњЪлСПЕФЦНОљдТдіГЄТЪЃЛ
ЃЈ2ЃЉДгЫФдТЗнЦ№ЩЬГЁвђЛЛМОЧхВжВЩгУНЕМлДйЯњЕФЗНЪНЃЌОЕїВщЗЂЯжЃЌдкШ§дТЗнЯњСПЕФЛљДЁЩЯЃЌИУЗўзАЪлМлУПНЕМл5дЊЃЌдТЯњЪлСПдіМг10МўЃЌЕБУПМўНЕМлЖрЩйдЊЪБЃЌЫФдТЗнПЩЛёРћ12000дЊЃП
ЁОД№АИЁПЃЈ1ЃЉЖўЁЂШ§дТЗнЯњЪлСПЕФЦНОљдТдіГЄТЪЮЊ25%ЃЛЃЈ2ЃЉУПМўНЕМл50дЊЃЌЫФдТЗнПЩЛёРћ12000дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩЕУЃКвЛдТЗнЕФЯњЪлСПЮЊЃК320МўЃЛЩшЖўдТЗнЕНШ§дТЗнЯњЪлЖюЕФдТЦНОљдіГЄТЪЃЌдђЖўдТЗнЕФЯњЪлСПЮЊЃК320ЃЈ1+xЃЉЃЛШ§дТЗнЕФЯњЪлСПЮЊЃК320ЃЈ1+xЃЉЃЈ1+xЃЉЃЌгжжЊШ§дТЗнЕФЯњЪлСПЮЊЃК500дЊЃЌгЩДЫЕШСПЙиЯЕСаГіЗНГЬЧѓГіxЕФжЕЃЌМДЧѓГіСЫЦНОљдіГЄТЪЃЛ
ЃЈ2ЃЉРћгУЯњСПЁСУПМўЩЬЦЗЕФРћШѓ=12000ЧѓГіМДПЩЃЎ
ЃЈ1ЃЉНтЃКЩшЖўЁЂШ§дТЗнЯњЪлСПЕФЦНОљдТдіГЄТЪЮЊxЃЌИљОнЬтвтЕУЃК
320ЃЈ1+xЃЉ2=500
НтЕУЃКx1=0.25ЃЌx2=-2.25ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
Д№ЃКЖўЁЂШ§дТЗнЯњЪлСПЕФЦНОљдТдіГЄТЪЮЊ25%ЃЎ
ЃЈ2ЃЉНтЃКЩшУПМўНЕМлyдЊЃЌИљОнЬтвтЕУЃК
ЃЈ500+10ЁС![]() ЃЉЃЈ150-y-80ЃЉ=12000
ЃЉЃЈ150-y-80ЃЉ=12000
ећРэЕУЃКy2+180y-11500=0
НтЕУЃКy1=50ЃЌy2=-230ЃЈВЛКЯЃЌЩсШЅЃЉЃЎ
Д№ЃКУПМўНЕМл50дЊЃЌЫФдТЗнПЩЛёРћ12000дЊЃЎ


 ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
ПкЫуЬтПЈББОЉИОХЎЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫШУбЇЩњФмИќМгСЫНтЮТжнРњЪЗЃЌФГаЃзщжЏЦпФъМЖЪІЩњЙВ480ШЫВЮЙлЮТжнВЉЮяЙнЃЎбЇаЃЯђзтГЕЙЋЫОзтСоAЁЂBСНжжГЕаЭНгЫЭЪІЩњЭљЗЕЃЌШєзтгУAаЭГЕ3СОЃЌBаЭГЕ6СОЃЌдђПегр15ИізљЮЛЃЛШєзтгУAаЭГЕ5СОЃЌBаЭГЕ4СОЃЌдђ15ШЫУЛзљЮЛЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНжжГЕаЭИїгаЖрЩйИізљЮЛЃЛ
ЃЈ2ЃЉШєAаЭГЕШезтН№ЮЊ350дЊЃЌBаЭГЕШезтН№ЮЊ400дЊЃЌЧвзтГЕЙЋЫОзюЖрФмЬсЙЉ7СОBаЭГЕЃЌгІдѕбљзтГЕФмЪЙзљЮЛЧЁКУзјТњЧвзтН№зюЩйЃЌВЂЧѓГізюЩйзтН№ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЎШчЭМЃЌОиаЮABCDжаЃЌOЮЊACжаЕуЃЌЙ§ЕуOЕФжБЯпЗжБ№гыABЁЂCDНЛгкЕуEЁЂFЃЌСЌНсBFНЛACгкЕуMЃЌСЌНсDEЁЂBOЃЎШєЁЯCOB=60ЁуЃЌFO=FCЃЌдђЯТСаНсТлЃКЂйFBДЙжБЦНЗжOCЃЛЂкЁїEOBЁеЁїCMBЃЛЂлDE=EFЃЛЂмSЁїAOEЃКSЁїBCM=2ЃК3ЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ

A. 4Иі B. 3Иі C. 2Иі D. 1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
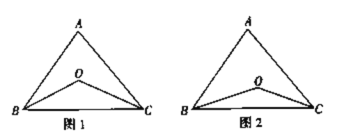
ЁОЬтФПЁПвбжЊШЮвтвЛИіШ§НЧаЮЕФШ§ИіФкНЧЕФКЭЪЧ180ЁуЃЌШчЭМ1ЃЌдкABCжаЃЌЁЯABCЕФНЧЦНЗжЯпBOгыЁЯACBЕФНЧЦНЗжЯпCOЕФНЛЕуЮЊO.
ЃЈ1ЃЉШєЁЯA=70ЁуЃЌЧѓЁЯBOCЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЁЯA=ІСЃЌЧѓЁЯBOCЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєBOЁЂCOЗжБ№ЪЧЁЯABCЁЂЁЯACBЕФШ§ЕШЗжЯпЃЌвВОЭЪЧЁЯOBC=![]() ЁЯABCЃЌЁЯOCB=
ЁЯABCЃЌЁЯOCB=![]() ЁЯACBЃЌЁЯA=ІСЃЌЧѓЁЯBOCЕФЖШЪ§.
ЁЯACBЃЌЁЯA=ІСЃЌЧѓЁЯBOCЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМEЁЂFЗжБ№дке§ЗНаЮABCDЕФБпBCЁЂCDЩЯЃЌЧвЁЯEAF=45ЁуЃЎ
ЃЈ1ЃЉЧѓжЄЃКEF=BE+DFЃЛ
ЃЈ2ЃЉШєЯпЖЮEFЁЂABЕФГЄЗжБ№ЪЧЗНГЬx2Љ5x+6=0ЕФСНИіИљЃЌЧѓЁїAEFЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЁѕABCDЕФСНБпABЃЌADЕФГЄЪЧЙигкxЕФЗНГЬx2ЃmxЃЋ![]() Ѓ
Ѓ![]() ЃН0ЕФСНИіЪЕЪ§ИљЃЎ
ЃН0ЕФСНИіЪЕЪ§ИљЃЎ
(1)ЕБmЮЊКЮжЕЪБЃЌЫФБпаЮABCDЪЧСтаЮЃПЧѓГіетЪБСтаЮЕФБпГЄЃЛ
(2)ШєABЕФГЄЮЊ2ЃЌФЧУДЁѕABCDЕФжмГЄЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩфЪждкЭЌвЛЬѕМўЯТНјааЩфЛїЃЌНсЙћШчЯТБэЫљЪОЃК

(1)МЦЫуВЂЬюаДБэжаЛїжаАааФЕФЦЕТЪЃЛЃЈНсЙћБЃСєШ§ЮЛаЁЪ§ЃЉ
(2)етИіЩфЪжЩфЛївЛДЮЃЌЛїжаАааФЕФИХТЪЙРМЦжЕЪЧЖрЩйЃПЃЈНсЙћБЃСєСНЮЛаЁЪ§ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
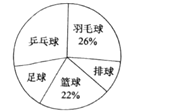
ЁОЬтФПЁПФГжабЇЮЊСЫСЫНтбЇЩњзюЯВЛЖЕФвЛжжЧђРрдЫЖЏЃЌвдБуКЯРэАВХХЛюЖЏГЁЕиЃЌдкШЋаЃжСЩйЯВЛЖвЛжжЧђРрЃЈЦЙХвЧђЁЂг№УЋЧђЁЂХХЧђЁЂРКЧђЁЂзуЧђЃЉдЫЖЏЕФ1500УћбЇЩњжаЃЌЫцЛњГщШЁСЫШєИЩУћбЇЩњНјааЕїВщЃЈУПШЫжЛФмдкетЮхжжЧђРрдЫЖЏжабЁдёвЛжжЃЉ.ЕїВщНсЙћЭГМЦШчЯТЃК
ЧђРрУћГЦ | ШЫЪ§ |
ЦЙХвЧђ | 42 |
г№УЋЧђ | a |
ХХЧђ | 15 |
РКЧђ | 33 |
зуЧђ | b |
![]()
НтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮГщбљЕїВщжаЕФбљБОЪЧ________ЃЛ
ЃЈ2ЃЉЭГМЦБэжаЃЌa=________ЃЌb=________ЃЛ
ЃЈ3ЃЉЪдЙРМЦЩЯЪі1500УћбЇЩњжазюЯВЛЖЦЙХвЧђдЫЖЏЕФШЫЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЯюЙЄГЬМзЖгЕЅЖРЭъГЩЫљашЬьЪ§ЪЧввЖгЕЅЖРЭъГЩетЯюЙЄГЬЫљашЬьЪ§ЕФ![]() ЃЛШєгЩввЖгЯШзі45ЬьЃЌЪЃЯТЕФЙЄГЬдйгЩМзЁЂввСНЖгКЯзї54ЬьПЩвдЭъГЩЁЃ
ЃЛШєгЩввЖгЯШзі45ЬьЃЌЪЃЯТЕФЙЄГЬдйгЩМзЁЂввСНЖгКЯзї54ЬьПЩвдЭъГЩЁЃ
ЃЈ1ЃЉЧѓМзЁЂввСНЖгЕЅЖРЭъГЩетЯюЙЄГЬИїашвЊЖрЩйЬьЃП
ЃЈ2ЃЉвбжЊМзЖгУПЬьЕФЪЉЙЄЗбгУЮЊ0.82ЭђдЊЃЌввЖгУПЬьЕФЪЉЙЄЗбгУЮЊ0.68ЭђдЊЃЌЙЄГЬдЄЫуЕФЪЉЙЄЗбгУЮЊ100ЭђдЊ.ФтАВХХМзЁЂввСНЖгЭЌЪБКЯзїЭъГЩетЯюЙЄГЬЃЌдђЙЄГЬдЄЫуЕФЪЉЙЄЗбгУЪЧЗёЙЛгУЃПШєВЛЙЛгУЃЌашзЗМгдЄЫуЖрЩйЭђдЊЃПЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com