练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于的一元二次方程．

    （1）若此方程的一个根为1，求的值；

    （2）求证：不论取何实数，此方程都有两个不相等的实数根．

    【答案】（1）m=（2）证明见解析

    【解析】试题分析：一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．

    （1）直接把x=1代入方程x2+mx+m﹣2=0求出m的值；

    （2）计算出根的判别式，进一步利用配方法和非负数的性质证得结论即可．

    解：（1）根据题意，将x=1代入方程x2+mx+m﹣2=0，

    得：1+m+m﹣2=0，

    解得：m=；

    （2）∵△=m2﹣4×1×（m﹣2）=m2﹣4m+8=（m﹣2）2+4＞0，

    ∴不论m取何实数，该方程都有两个不相等的实数根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形 ABCD 中，∠BAD=α，∠BCD=180°-α，BD 平分∠ABC．

    （1）如图，若α=90°，根据教材中一个重要性质直接可得 DA=CD，这个性质是 ；

    （2）问题解决：如图，求证：AD=CD；

    （3）问题拓展：如图，在等腰△ABC 中，∠BAC=100°，BD 平分∠ABC，求证：BD+AD=BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    在数学课上，老师请同学思考如下问题：如图①，我们把一个四边形的四边中点依次连接起来得到的四边形是平行四边形吗？

    小敏在思考问题，有如下思路：连接．

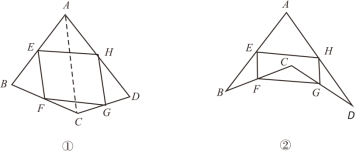
    结合小敏的思路作答．

    （1）若只改变图①中四边形的形状（如图②），则四边形还是平行四边形吗？说明理由；

    （参考小敏思考问题方法）

    （2）如图②，在（1）的条件下，若连接．

    ①当与满足什么条件时，四边形是矩形，写出结论并证明；

    ②当与满足____时，四边形是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线的顶点为（1，﹣4），且过点（﹣2，5）．

    （1）求抛物线解析式；

    （2）直接写出当函数值y＞0时，自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．

    （1）根据图象信息，当t＝　 　分钟时甲乙两人相遇，甲的速度为　 　米/分钟，乙的速度为　 　米/分钟；

    （2）图中点A的坐标为　 　；

    （3）求线段AB所直线的函数表达式；

    （4）在整个过程中，何时两人相距400米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC＝2，∠BAC＝30°，则线段PM的最大值是（　　）

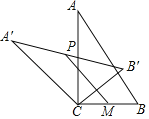
    A.4B.3C.2D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.

    （1）求证：OE是CD的垂直平分线.

    （2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB和DE是直立在地面上的两根立柱．AB=4m，某一时刻AB在阳光下的投影BC=3m．

    （1）请你在图中画出此时DE在阳光下的投影．

    （2）在测量AB的投影时，同时测量出DE在阳光下的投影长为8m，请你计算DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=BC=1，则下列结论：

    ①∠CAD=30°②BD=③S平行四边形ABCD=ABAC④OE=AD⑤S△APO=，正确的个数是（　　）

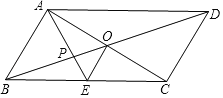
    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    同步练习册答案