
【题目】已知抛物线的顶点为(1,﹣4),且过点(﹣2,5).
(1)求抛物线解析式;
(2)直接写出当函数值y>0时,自变量x的取值范围.
科目:初中数学 来源: 题型:
【题目】亚奥理事会于![]() 年
年![]() 月3
月3![]() 日在土库曼斯坦阿什哈巴德举行第
日在土库曼斯坦阿什哈巴德举行第![]() 届代表大会,并在会上投票选出
届代表大会,并在会上投票选出![]() 年第
年第![]() 届亚运会举办城市为杭州.
届亚运会举办城市为杭州.![]() 个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间
个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间![]() 年
年![]() 月
月![]() 日
日![]() 时应是( ).
时应是( ).

A.伦敦时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
B.巴黎时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
C.智利时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
D.曼谷时间![]() 年
年![]() 月
月![]() 日
日![]() 时
时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )
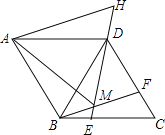
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,为响应号召,某商场计划购进甲,乙两种节能灯共200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 20 | 30 |
乙型 | 30 | 45 |
(1)若购进甲,乙两种节能灯共用去5200元,求甲、乙两种节能灯各进多少只?
(2)若商场准备用不多于5400元购进这两种节能灯,问甲型号的节能灯至少进多少只?
(3)在(2)的条件下,该商场销售完200只节能灯后能否实现盈利超过2690元的目标?若能请你给出相应的采购方案;若不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2…、正方形AnBnnCn﹣1按如图方式放置,点A1、A2、A3、…在直线y=x+1上,点C1、C2、C3、…在x轴上.已知A1点的坐标是(0,1),则点B3的坐标为_____,点Bn的坐标是_____.
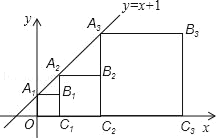
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
问:(1)这个小组男生的达标率为多少?(达标率=![]() )
)
(2)这个小组男生的平均成绩是多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com