
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2…、正方形AnBnnCn﹣1按如图方式放置,点A1、A2、A3、…在直线y=x+1上,点C1、C2、C3、…在x轴上.已知A1点的坐标是(0,1),则点B3的坐标为_____,点Bn的坐标是_____.
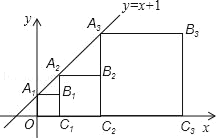
【答案】(7,4) (2n﹣1,2n﹣1).
【解析】
根据一次函数图象上点的坐标特征可得出点A1的坐标,结合正方形的性质可得出点B1的坐标,同理可得出点B2、B3、B4、…的坐标,再根据点的坐标的变化即可找出点Bn的坐标.
当x=0时,y=x+1=1,
∴点A1的坐标为(0,1).
∵四边形A1B1C1O为正方形,
∴点B1的坐标为(1,1).
当x=1时,y=x+1=2,
∴点A2的坐标为(1,2).
∵四边形A2B2C2C1为正方形,
∴点B2的坐标为(3,2).
同理可得:点A3的坐标为(3,4),点B3的坐标为(7,4),点A4的坐标为(7,8),点B4的坐标为(15,8),…,
∴点Bn的坐标为(2n﹣1,2n﹣1).
故答案为:(7,4), (2n﹣1,2n﹣1)


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
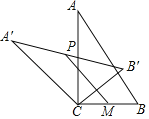
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:

解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a=________,b=________.
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O在线段AB上,AB=6,OC为射线,且∠BOC=45°.动P以每秒1个单位长度的速度从点O出发,沿射线OC做匀速运动.设运动时间为t 秒.

(1)如图1,若AO=2.
①当 t=6秒时,则OP= ,S△ABP= ;
②当△ABP与△PBO相似时,求t的值;
(2)如图2,若点O为线段AB的中点,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人往一艘轮船上装载货物,装完货物所需时间 y(分钟)与装载速度 x(吨/分钟)之间的函数关系如图.
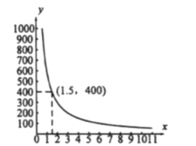
(1)求y与x之间的函数表达式:
(2)若要求在2小时至2.5小时内(包括2小时与2.5小时)装完这批货物,求装货速度的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com