
����Ŀ��Ŀǰ���ܵ��ڳ����ѻ����ռ���Ϊ��Ӧ���٣�ij�̳��ƻ������ף������ֽ��ܵƹ�200ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���
���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� | |
���� | 20 | 30 |
���� | 30 | 45 |
��1���������ף������ֽ��ܵƹ���ȥ5200Ԫ����ס������ֽ��ܵƸ�������ֻ��
��2�����̳����ò�����5400Ԫ���������ֽ��ܵƣ��ʼ��ͺŵĽ��ܵ����ٽ�����ֻ��
��3���ڣ�2���������£����̳�������200ֻ���ܵƺ��ܷ�ʵ��ӯ������2690Ԫ��Ŀ�ꣿ�������������Ӧ�IJɹ�������������˵������.
���𰸡���1�����ֽ��ܵ���80ֻ�������ֽ��ܵ���120ֻ����2�����ͺŵĽ��ܵ����ٽ�60ֻ����3�������֣���![]() ʱ���ɹ������ͺŵĽ��ܵ�60̨�������ͺŵĽ��ܵ�140̨����
ʱ���ɹ������ͺŵĽ��ܵ�60̨�������ͺŵĽ��ܵ�140̨����![]() ʱ���ɹ������ͺŵĽ��ܵ�61̨�������ͺŵĽ��ܵ�139̨
ʱ���ɹ������ͺŵĽ��ܵ�61̨�������ͺŵĽ��ܵ�139̨
��������
��1������ֽ��ܵ���![]() ֻ�������ֽ��ܵ���
ֻ�������ֽ��ܵ���![]() ֻ�����������г�����x��y�Ķ�Ԫһ�η����������⼴�ɣ�
ֻ�����������г�����x��y�Ķ�Ԫһ�η����������⼴�ɣ�
��2������ֽ��ܵ���![]() ֻ�������ֽ��ܵ���
ֻ�������ֽ��ܵ���![]() ֻ�����������г�����m��һԪһ�β���ʽ������⼴�ɣ�
ֻ�����������г�����m��һԪһ�β���ʽ������⼴�ɣ�
��3������������в���ʽ![]() �����m��ȡֵ��Χ���ٽ�ϣ�2��ȡm������ֵ����.
�����m��ȡֵ��Χ���ٽ�ϣ�2��ȡm������ֵ����.
�⣺����ֽ��ܵ���![]() ֻ�������ֽ��ܵ���
ֻ�������ֽ��ܵ���![]() ֻ��������ã�
ֻ��������ã�
![]() ��
��
��ã�![]() ��
��
�𣺼��ֽ��ܵ���80ֻ�������ֽ��ܵ���120ֻ��
��2������ֽ��ܵ���![]() ֻ�������ֽ��ܵ���
ֻ�������ֽ��ܵ���![]() ֻ. ��������ã�
ֻ. ��������ã�
![]() ��
��
��ã�![]() ��
��
�𣺼��ͺŵĽ��ܵ����ٽ�60ֻ��
��3�������⣬��
![]() ��
��
��ã�![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��������
��������
��![]() ��
��
��Ӧ���������֣���![]() ʱ���ɹ������ͺŵĽ��ܵ�60̨�������ͺŵĽ��ܵ�140̨����
ʱ���ɹ������ͺŵĽ��ܵ�60̨�������ͺŵĽ��ܵ�140̨����![]() ʱ���ɹ������ͺŵĽ��ܵ�61̨�������ͺŵĽ��ܵ�139̨��
ʱ���ɹ������ͺŵĽ��ܵ�61̨�������ͺŵĽ��ܵ�139̨��


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAC��ƽ������BC�Ĵ�ֱƽ�����ཻ�ڵ�D��DE��AB��DF��AC������ֱ�ΪE��F��AB=11��AC=5����BE=______________��
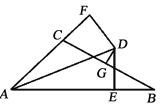
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������ȤС���ڱ�Уѧ���п�չ���ж��й�2014����������Ƚ��¼�֪�����ר���������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����ΪA��B��C��D���࣮���У�A���ʾ���dz��˽�����B���ʾ���Ƚ��˽�����C���ʾ�������˽�����D���ʾ����̫�˽�������������������������±���
��� | A | B | C | D |
Ƶ�� | 30 | 40 | 24 | b |
Ƶ�� | a | 0.4 | 0.24 | 0.06 |

��1�����е�a=________��b=________��
��2�����ݱ������ݣ�������ͳ��ͼ�����ΪB��ѧ��������Ӧ������Բ�ĽǵĶ�����
��3������У��ѧ��1000�������ݵ��������Ƹ�Уѧ�������ΪC������ԼΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��AC����O�����ڵ�B��C����A=50������P��Բ������B��C��һ���㣬����BPC�Ķ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߵĶ���Ϊ��1����4�����ҹ��㣨��2��5����
��1���������߽���ʽ��
��2��ֱ��д��������ֵy��0ʱ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������뻷������һ������Ϸ,��Ϸ�������£�ÿ�˴�1,2,3,4,5,6,7,8������ѡ��һ������,Ȼ�����˸�ת��һ����ͼ��ʾ��ת�̣�ת�̱���Ϊ�����ȵ��ĸ����Σ�,����ת��������֮�͵���˭����ѡ�����,˭�ͻ�ʤ��������ת��������֮�Ͳ��������Ǹ���ѡ�����,������һ��������Ϸ,ֱ������ʤ��.����������ѡ�������5,���б�������״ͼ�ķ���,������ʤ�ĸ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90��������ABC�ƶ���C��ʱ����ת�õ���A'B'C��M��BC���е㣬P��A'B'���е㣬����PM����BC��2����BAC��30�������߶�PM�����ֵ�ǣ�������
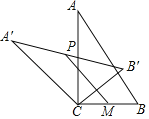
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�ͳ����ÿ��ӪҵԱ��ij�µ����۶���������µ�����ͳ��ͼ�Լ�������������ͳ��ͼ��

����������⣺
��1����ӪҵԱ�������۶�Ϊx����λ����Ԫ�����̳��涨����x��15ʱΪ����ְ����15��x��20ʱ��Ϊ������ְ����20��x��25Ϊ��ְ����x��25ʱΪ���㣮������ͳ��ͼ�е�a=________��b=________��
��2������ӪҵԱ�����۶����λ���������ֱ��Ƕ��٣�
��3��Ϊ�˵���ӪҵԱ�Ļ����ԣ������ƶ�һ�������۶��������������������ӪҵԱ���ܵ����������Ҫʹ��ӪҵԱ�İ��������ܻ�������Ӧ��Ϊ������Ԫ�������������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��
��![]() ����
����![]() �㣬��
�㣬��![]() ����
����![]() �㣬
�㣬 ![]() Ϊ
Ϊ![]() ���е㣬
���е㣬 ![]() Ϊ����
Ϊ����![]() ��һ�㣬��
��һ�㣬��![]() ����
����![]() ��
��![]() ��˳ʱ����ת
��˳ʱ����ת![]() ���߶�
���߶�![]() ����
����![]() ����СֵΪ__________.
����СֵΪ__________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com