
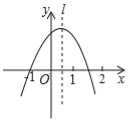
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
【答案】D.
【解析】
试题分析:①∵二次函数图象的开口向下,
∴a<0,
∵二次函数图象的对称轴在y轴右侧,
∴﹣![]() >0,
>0,
∴b>0,
∵二次函数的图象与y轴的交点在y轴的正半轴上,
∴c>0,
∴abc<0,故①错误;
②∵抛物线y=ax2+bx+c经过点(﹣1,0),
∴a﹣b+c=0,故②正确;
③∵a﹣b+c=0,∴b=a+c.
由图可知,x=2时,y<0,即4a+2b+c<0,
∴4a+2(a+c)+c<0,
∴6a+3c<0,∴2a+c<0,故③正确;
④∵a﹣b+c=0,∴c=b﹣a.
由图可知,x=2时,y<0,即4a+2b+c<0,
∴4a+2b+b﹣a<0,
∴3a+3b<0,∴a+b<0,故④正确.
故选D.


科目:初中数学 来源: 题型:
【题目】规定:如果关于的一元二次方程![]() 有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:
①方程![]() 是倍根方程;
是倍根方程;
②若关于的方程![]() 是倍根方程,则a=±3;
是倍根方程,则a=±3;
③若关于x的方程![]() 是倍根方程,则抛物线
是倍根方程,则抛物线![]() 与x轴的公共点的坐标是(2,0)和(4,0);
与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数![]() 的图象上,则关于x的方程
的图象上,则关于x的方程![]() 是倍根方程
是倍根方程
上述结论中正确的有( )
A.①② B.③④ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,AO是高,D为AO上一点,以CD为一边,在CD下方作等边△CDE,连接BE.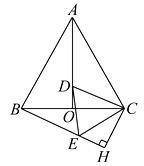
(1)求证:AD=BE;
(2)过点C作CH⊥BE,交BE的延长线于H,若BC=8,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量;无人机在A处正上方97m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测),无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.
(1)求主桥AB的长度;
(2)若两观察点P、D的连线与水平方向的夹角为30°,求引桥BC的长.
(长度均精确到1m,参考数据:![]() ≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年10月1日,重庆四大景区共接待游客约518 000人,这个数可用科学记数法表示为( )
A.0.518×104
B.5.18×105
C.51.8×106
D.518×103
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com