
【题目】已知△ABC内接于⊙O,过点A作直线EF.

(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射手在同一条件下进行射击,结果如下表所示:

(1)计算并填写表中击中靶心的频率;(结果保留三位小数)
(2)这个射手射击一次,击中靶心的概率估计值是多少?(结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1500名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 人数 |
乒乓球 | 42 |
羽毛球 | a |
排球 | 15 |
篮球 | 33 |
足球 | b |
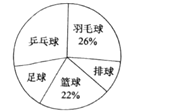
![]()
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,a=________,b=________;
(3)试估计上述1500名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
频率分布表
分组 | 频数 | 百分比 |
144.5~149.5 | 2 | 4% |
149.5~154.5 | 3 | 6% |
154.5~159.5 | a | 16% |
159.5~164.5 | 17 | 34% |
164.5~169.5 | b | n% |
169.5~174.5 | 5 | 10% |
174.5~179.5 | 3 | 6% |
(1)求a、b、n的值;
(2)补全频数分布直方图;
(3)学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?
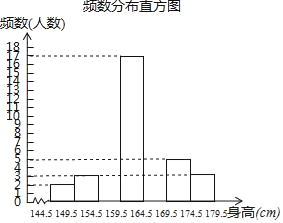
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如左图,某小区的平面图是一个400×300平方米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%,并且南北空地与东西空地的宽度各自相同.
(1)求该小区南北空地的宽度;
(2)如右图,该小区在东西南三块空地上做如图所示的矩形绿化带,绿化带与建筑区之间为小区道路,小区道路宽度一致.已知东西侧绿化带完全相同,其长约为200米,南侧绿化带的长为300米,绿化面积为18000平方米,请求出小区道路的宽度.
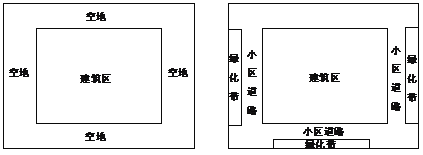
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程甲队单独完成所需天数是乙队单独完成这项工程所需天数的![]() ;若由乙队先做45天,剩下的工程再由甲、乙两队合作54天可以完成。
;若由乙队先做45天,剩下的工程再由甲、乙两队合作54天可以完成。
(1)求甲、乙两队单独完成这项工程各需要多少天?
(2)已知甲队每天的施工费用为0.82万元,乙队每天的施工费用为0.68万元,工程预算的施工费用为100万元.拟安排甲、乙两队同时合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的 ⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长.
的长.
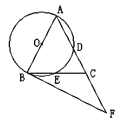
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com