练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在 Rt△ABC 中，∠BAC=90°，AB=6,AC=8,D 为 AC 上一点，将△ABD 沿 BD 折叠，使点 A 恰好落在 BC 上的 E 处，则折痕 BD 的长是（ ）

    A.5B.C.3 D.

    【答案】C

    【解析】

    根据勾股定理易求BC=10．根据折叠的性质有AB=BE，AD=DE，∠A=∠DEB=90°,
    在△CDE中，设AD=DE=x，则CD=8-x，EC=10-6=4．根据勾股定理可求x,在△ADE中，运用勾股定理求BD．

    解：∵∠A=90°，AB=6,AC=8，
    ∴BC=10．
    根据折叠的性质，AB=BE，AD=DE，∠A=∠DEB=90°．
    ∴EC=10-6=4．
    在△CDE中，设AD=DE=x，则CD=8-x，根据勾股定理得
    （8-x）2=x2+42．
    解得x=3．
    ∴DE=3．
    ∴BD==3,故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：

    在数学课上，老师请同学思考如下问题：如图①，我们把一个四边形的四边中点依次连接起来得到的四边形是平行四边形吗？

    小敏在思考问题，有如下思路：连接．

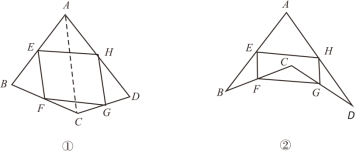
    结合小敏的思路作答．

    （1）若只改变图①中四边形的形状（如图②），则四边形还是平行四边形吗？说明理由；

    （参考小敏思考问题方法）

    （2）如图②，在（1）的条件下，若连接．

    ①当与满足什么条件时，四边形是矩形，写出结论并证明；

    ②当与满足____时，四边形是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.

    （1）求证：OE是CD的垂直平分线.

    （2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB和DE是直立在地面上的两根立柱．AB=4m，某一时刻AB在阳光下的投影BC=3m．

    （1）请你在图中画出此时DE在阳光下的投影．

    （2）在测量AB的投影时，同时测量出DE在阳光下的投影长为8m，请你计算DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD是边长为4的正方形，点E在边AD所在的直线上，连接CE，以CE为边，作正方形CEFG(点D，点F在直线CE的同侧)，连接BF，

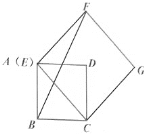
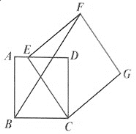
    图1 图2

    (1)如图1，当点E与点A重合时，则_____；

    (2)如图2，当点E在线段AD上时，，

    ①求点F到AD的距离；

    ②求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点O在线段AB上，AB=6，OC为射线，且∠BOC=45°．动P以每秒1个单位长度的速度从点O出发，沿射线OC做匀速运动．设运动时间为t 秒．

    （1）如图1，若AO=2．

    ①当 t=6秒时，则OP= ，S△ABP= ；

    ②当△ABP与△PBO相似时，求t的值；

    （2）如图2，若点O为线段AB的中点，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求AQBP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，DF交BC于点E．

    （1）求证：△DCE≌△BFE；

    （2）若CD=2，∠ADB=30°，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=BC=1，则下列结论：

    ①∠CAD=30°②BD=③S平行四边形ABCD=ABAC④OE=AD⑤S△APO=，正确的个数是（　　）

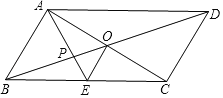
    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料并解决问题

    进位制是一种记数方式，可以用有限的数字符号代表所有的数值，使用数字符号的数目称为基数，基数为n，即可称n进制。现在最常用的是十进制，通常使用10个阿拉伯数字0~9进行记数，特点是逢十进一。

    对于任意一个用进制表示的数，通常使用n个阿拉伯数字进行记数，特点是逢n进一。我们可以通过以下方式把它转化为十进制：

    例如：五进制数，记作: ，

    七进制数，记作:

    （1）请将以下两个数转化为十进制： ____________， ____________ ；

    （2）若一个正数可以用七进制表示为，也可以用五进制表示为，请求出这个数并用十进制表示。

    查看答案和解析>>

    同步练习册答案