
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
【答案】(1)(﹣3,1),(﹣2,﹣2),(﹣1,﹣1);(2)先向左平移4个单位,再向下平移2个单位;(3)(a﹣4,b﹣2).(4)2
【解析】
试题分析:(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据对应点A、A′的变化写出平移方法即可;
(3)根据平移规律逆向写出点P′的坐标;
(4)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
试题解析:1)A′(﹣3,1); B′(﹣2,﹣2);C′(﹣1,﹣1);
(2)先向左平移4个单位,再向下平移2个单位;
或:先向下平移2个单位,再向左平移4个单位;
(3)P′(a﹣4,b﹣2);
(4)△ABC的面积=2×3﹣![]() ×1×3﹣
×1×3﹣![]() ×1×1﹣
×1×1﹣![]() ×2×2
×2×2
=6﹣1.5﹣0.5﹣2
=2.


科目:初中数学 来源: 题型:
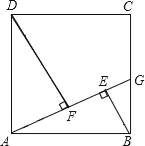
【题目】如图,在边长为4的正方形ABCD中,点G是BC边上的任意一点(不同于端点B、C),连接AG,过B、D两点作BE⊥AG,DF⊥AG,垂足分为E、F.
(1)求证:△ABE≌△DAF;
(2)若△ADF的面积为1,试求|BE﹣DF|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
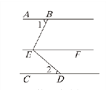
【题目】如图,AB∥CD∥EF,∠1=75,∠2=45,点 G为∠BED 内一点,且 EG把∠BED分成 1 ∶ 2 两部分,则∠GEF 的度数为 ___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:
2 | 6 | 18 | 54 | 162…① |
-1 | 3 | 15 | 51 | 159…② |
-1 | -3 | -9 | -27 | -81…③ |
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数有什么关系?
(3)每行取第6个数计算它们的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com