
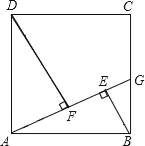
【题目】如图,在边长为4的正方形ABCD中,点G是BC边上的任意一点(不同于端点B、C),连接AG,过B、D两点作BE⊥AG,DF⊥AG,垂足分为E、F.
(1)求证:△ABE≌△DAF;
(2)若△ADF的面积为1,试求|BE﹣DF|的值.
【答案】(1)证明见解析(2)2![]()
【解析】试题分析:
(1)由已知条件易得:∠DFA=∠AEB=∠DAB=90°,从而可得∠ADF+∠DAF=∠DAF+∠BAE=90°,由此即可得到∠ADF=∠BAE,结合正方形ABCD中AD=AB即可证得△ABE≌△DAF;
(2)设AF=a,DF=b,则由△ADF的面积为1可得![]() ,即可得到
,即可得到![]() ;由正方形的边长为4在Rt△ADF中可得:
;由正方形的边长为4在Rt△ADF中可得: ![]() ,由此即可得到
,由此即可得到![]() ,即可解得
,即可解得![]() 的值,从而可由|BE﹣DF|=|AF﹣DF|求出所求的值.
的值,从而可由|BE﹣DF|=|AF﹣DF|求出所求的值.
试题解析:
(1)在正方形ABCD中,∠DAB=90°,AB=AD,
∴∠DAF+∠BAE=90°,
∵DF⊥AG,BE⊥AG,
∴∠AFD=∠BEA=90°,∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中, 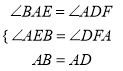 ,
,
∴△ABE≌△DAF(AAS);

(2)∵△ABE≌△DAF,
∴BE=AF,
设AF=a,DF=b,
∵△ADF的面积为1,
∴![]() AFDF=1,即
AFDF=1,即![]() ab=1,
ab=1,
∴ ab=2,
在Rt△ADF中,根据勾股定理得,AF2+DF2=AD2,即a2+b2=42=16,
∴(a﹣b)2=a2﹣2ab+b2=16﹣4=12,
∴|a﹣b|=![]() ,即|AF﹣DF|=|BE﹣DF|=
,即|AF﹣DF|=|BE﹣DF|=![]() .
.


科目:初中数学 来源: 题型:
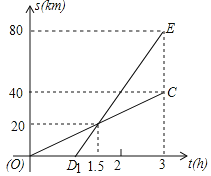
【题目】已知A、B两地相距80km,甲、乙两人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DE、OC分别表示甲、乙两人离开A地的距离(km)与乙出发的时间(h)的关系,根据图象填空:
(1)乙先出发__h后,甲才出发;
(2)大约在乙出发后__h,两人相遇,这时他们离A地__km;
(3)甲到达B地时,乙离开A地__km;
(4)甲的速度是__km/h;乙的速度是__km/h;
(5)甲离开A地的距离s(km)与乙出发的时间t(h)的关系式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
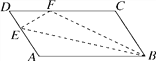
【题目】如图,在□ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为22,则□ABCD的周长为________,FC的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填在相应的括号内.
-![]() ,0,0.16,3
,0,0.16,3![]() ,
, ![]() ,-
,-![]() ,
, ![]() ,
,![]() ,-
,-![]() ,-3.14
,-3.14
有理数:{____________________________________________________};
无理数:{____________________________________________________};
负实数:{____________________________________________________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、 ![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ![]() ,0),B(0,2),则点B2016的坐标为 .
,0),B(0,2),则点B2016的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 ![]() BF长为半径画弧,两弧交于一点P,连
BF长为半径画弧,两弧交于一点P,连
接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为 , ∠ABC=°.(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
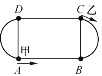
【题目】如图,点A、B、C、D把一个400米的环形跑道分成相等的4段,即两条直道和两条弯道的长度相同.甲平均每秒跑4米,乙平均每秒跑6米,若甲、乙两人分别从A、C两处同时相向出发(如图),当他们第4次相遇时,其相遇点在____________段(填”AB”或”BC”或”CD”或”DA”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com