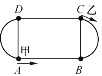
【题目】如图，点A、B、C、D把一个400米的环形跑道分成相等的4段，即两条直道和两条弯道的长度相同．甲平均每秒跑4米，乙平均每秒跑6米，若甲、乙两人分别从A、C两处同时相向出发(如图)，当他们第4次相遇时，其相遇点在____________段(填”AB”或”BC”或”CD”或”DA”)．
【答案】BC
【解析】甲乙两人分别从A、C两处同时相向出发，从图上可知首次相遇是个相遇问题，找到路程，知道速度，根据路程=速度×时间，可列方程求解；再次相遇仍旧是个相遇问题，找到路程，知道速度，根据路程=速度×时间，可列方程求解；找到每次相遇时间的规律，可求出相遇4次所用的时间，然后根据时间求出甲所跑的位置，从而求解．
设两人第一次相遇时跑了x秒，则有4x+6x=200，
解得：x=20，
第1次相遇，总用时20秒，
依此类推可得：
第2次相遇，总用时20+20×2，即60秒，
第3次相遇，总用时20+20×4，即100秒，
第4次相遇，总用时20+20×6，即140秒，
则此时甲跑的圈数为140×4÷400=1.4，
400×0.4=160米，
此时甲在BC弯道上，
故答案为：BC.
举一反三单元同步过关卷系列答案科目：初中数学 来源： 题型：
【题目】如图，甲、乙两艘轮船同时从港口O出发，甲轮船以20海里/时的速度向南偏东45°方向航行，乙轮船向南偏西45°方向航行．已知它们离开港口O两小时后，两艘轮船相距50海里，求乙轮船平均每小时航行多少海里？
查看答案和解析>>
科目：初中数学 来源： 题型：
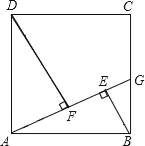
【题目】如图，在边长为4的正方形ABCD中，点G是BC边上的任意一点（不同于端点B、C），连接AG，过B、D两点作BE⊥AG，DF⊥AG，垂足分为E、F．
（1）求证：△ABE≌△DAF；
（2）若△ADF的面积为1，试求|BE﹣DF|的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知在平面直角坐标系中，O是坐标原点，点A（2，5）在反比例函数y= 
的图象上．一次函数y=x+b的图象过点A，且与反比例函数图象的另一交点为B．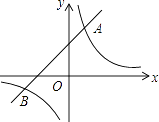
（1）求k和b的值；
（2）设反比例函数值为y1 ， 一次函数值为y2 ， 求y1＞y2时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)来表示．例如f(x)＝x2＋3x－5，把x＝某数时多项式的值用f(某数)来表示．例如x＝－1时多项式x2＋3x－5的值记为f(－1)＝(－1)2＋3×(－1)－5＝－7.
(1)已知g(x)＝－2x2－3x＋1，分别求出g(－1)和g(－2)；
(2)已知h(x)＝ax3＋2x2－ax－6，当h(
)＝a，求a的值；
(3)已知f(x)＝
－
－2(a，b为常数)，当k无论为何值，总有f(1)＝0，求a，b的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．
（1）求证：四边形BEDF是平行四边形；
（2）当四边形BEDF是菱形时，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC 中，AB＝AC，D 是直线 BC 上一点（不与点 B、C 重合），以 AD 为一边在 AD的右侧作△ADE，AD＝AE，∠DAE＝∠BAC，连接 CE.
（1）如图 1，当点 D 在线段 BC 上时，求证:△ABD≌△ACE；
（2）如图 2，当点 D 在线段 BC 上时，如果∠BAC＝90°，求∠BCE 的度数；
（3）如图 3，若∠BAC＝α，∠BCE＝β.点 D 在线段 CB 的延长线上时，则α、β之间有怎样 的数量关系？并证明你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
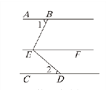
【题目】如图，AB∥CD∥EF，∠1＝75，∠2＝45，点 G为∠BED 内一点，且 EG把∠BED分成 1 ∶ 2 两部分,则∠GEF 的度数为 ___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
