【题目】某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．
（1）该商场两次共购进这种运动服多少套？
（2）如果这两批运动服每套的售价相同，且全部售完后总利润不低于20%，那么每套售价至少是多少元？
科目：初中数学 来源： 题型：
【题目】一方有难八方支援，某市政府筹集抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型可供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
(1)若全部物资都用甲、乙两种车来运送，需运费8200元，则分别需甲、乙两种车各几辆？
(2)为了节约运费，该市政府共调用16辆甲、乙，丙三种车都参与运送物资，试求出有几种运送方案，哪种方案的运费最省？其费用是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
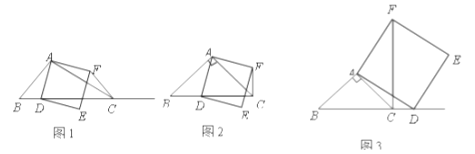
【题目】如图1，在
中，
为锐角，点
为射线
上一点，联结
，以为一边且在的右侧作正方形
．
（1）如果
，
，
①当点在线段上时（与点
不重合），如图2，线段
所在直线的位置关系为 ，线段的数量关系为 ；
②当点在线段的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；
（2）如果
，
是锐角，点在线段上，当满足什么条件时，
（点
不重合），并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用四个螺丝将四条不可弯曲的本条围成一个木框（形状不限），不记螺丝大小，其中相邻两螺丝之间的距离依次为3，4，5，7.且相邻两本条的夹角均可调整，若调整木条的夹角时不破坏此木框，则任意两个螺丝之间的最大距离是（ ）
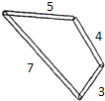
A.6B.7C.8D.9
查看答案和解析>>
科目：初中数学 来源： 题型：
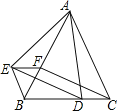
【题目】如图，△ABC和△BEF都是等边三角形，点D在BC边上，点F在AB边上，且∠EAD=60°，连接ED、CF.
（1）求证：△ABE≌△ACD；
（2）求证：四边形EFCD是平行四边形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并解决后面的问题.
材料：一般地，
个相同的因数
相乘：个记为
，如
，此时，3叫做以2为底8的对数，记为
（即
）.
一般地，若
（
且
，
），则叫做以为底
的对数，记为
（即
）.如
，则4叫做以3为底81的对数，记为
（即
）.
问题：（1）计算以下各对数的值：
________，
________，
________.
（2）观察（1）中三数4、16、64之间满足怎样的关系式？
、
、
之间又满足怎样的关系式？______________________________________________________________________________
（3）由（2）的结果，你能归纳出一个一般性的结论吗？
____________________（且，
，
）
（4）根据幂的运算法则：
以及对数的含义证明（3）中结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为准备参加某市2019年度中小学生机器人竞赛，学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化，各项量化满分100分，根据量化结果择优推荐.它们三项量化得分如下表：
量化项目 | 量化得分 | |
甲队 | 乙队 | |
创意 | 85 | 72 |
设计 | 70 | 66 |
编程与制作 | 64 | 84 |
（1）如果根据三项量化的平均分择优推荐，哪队将被推荐参赛？
（2）根据本次中小学生机器人竞赛的主题要求，如果学校根据创意、设计、编程与制作三项量化得分按
的比例确定每队最后得分的平均分择优推荐，哪队将被推荐参赛？并对另外一队提出合理化的建议.
查看答案和解析>>
科目：初中数学 来源： 题型：
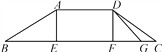
【题目】为了方便行人，市政府打算修建如图所示的过街天桥，桥面AD平行于地面BC，立柱AE⊥BC于点E，立柱DF⊥BC于点F，若AB＝5
米，tanB＝
，∠C＝30°.
(1)求桥面AD与地面BC之间的距离．
(2)因受地形限制，决定对该天桥进行改建，使CD斜面的坡度变陡，将其30°坡角改为40°，改建后斜面为DG，试计算此次改建节省路面宽度CG大约应是多少？(结果精确到0.1米，参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
