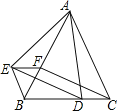
【题目】如图，△ABC和△BEF都是等边三角形，点D在BC边上，点F在AB边上，且∠EAD=60°，连接ED、CF.

（1）求证：△ABE≌△ACD；

（2）求证：四边形EFCD是平行四边形.

参考答案：

【答案】见解析

【解析】试题分析：(1)、根据等边三角形的性质得出∠EAB=∠CAD，∠EBA=∠ACB，从而得出三角形全等；(2)、根据三角形全等得出BE=CD，根据等边三角形的性质得出BE=EF，∠EFB=∠ABC，最后根据一组对边平行且相等得出平行四边形．

试题解析：(1)、∵△ABC和△BEF都是等边三角形，

∴AB=AC，∠EBF=∠ACB=∠BAC=60°， ∵∠EAD=60°， ∴∠EAD=∠BAC，

∴∠EAB=∠CAD， 在△ABE和△ACD中，∠EBA=∠ACB，AB=AC，∠EAB=∠DAC，

∴△ABE≌△ACD．

(2)、由（1）得△ABE≌△ACD， ∴BE=CD， ∵△BEF、△ABC是等边三角形，

∴BE=EF， ∴∠EFB=∠ABC=60°， ∴EF∥CD， ∴BE=EF=CD，

∴EF=CD，且EF∥CD， ∴四边形EFCD是平行四边形．

关闭