
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数 ;点P表示的数 (用含t的代数式表示)
(2)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是 .
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?
(4)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
![]()
【答案】(1)﹣14,8﹣5t;(2)11;(3)若点P、Q同时出发,2.5或3秒时P、Q之间的距离恰好等于2;(4)点P运动11秒时追上点Q.
【解析】
(1)根据已知可得B点表示的数为8-22;点P表示的数为8-5t;(2)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时两种情况求MN的长即可;(3)点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2,分①点P、Q相遇之前和②点P、Q相遇之后两种情况列方程求解即可;(4)点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC-BC=AB,列出方程求解即可.
(1)∵点A表示的数为8,B在A点左边,AB=22,
∴点B表示的数是8﹣22=﹣14,
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8﹣5t.
(2)①当点P在点A、B两点之间运动时:
![]()
MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)=![]() AB=
AB=![]() ×22=11,
×22=11,
②当点P运动到点B的左侧时:
![]()
MN=MP﹣NP=![]() AP﹣
AP﹣![]() BP=
BP=![]() (AP﹣BP)=
(AP﹣BP)=![]() AB=11,
AB=11,
∴线段MN的长度不发生变化,其值为11.
(3)若点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
由题意得3t+2+5t=22,解得t=2.5;
②点P、Q相遇之后,
由题意得3t﹣2+5t=22,解得t=3.
答:若点P、Q同时出发,2.5或3秒时P、Q之间的距离恰好等于2;
(4)设点P运动x秒时,在点C处追上点Q,
![]()
则AC=5x,BC=3x,
∵AC﹣BC=AB,
∴5x﹣3x=22,
解得:x=11,
∴点P运动11秒时追上点Q.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(﹣2,2),B(0,5),C(0,2).
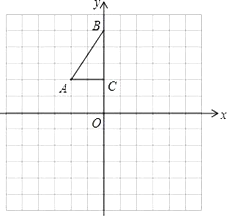
(1)画△A1B1C,使它与△ABC关于点C成中心对称;
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
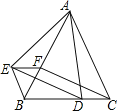
【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=4,BC=2.若把它放在平面直角坐标系中,使AB在x轴上,点C在y轴上,如果点A的坐标为(-3,0),求点B,C,D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com