
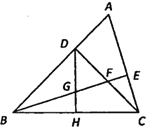
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
【答案】6
【解析】
求出 BG=GC,求出∠EGC=∠ECG,推出 CE=GE,进而利用等腰三角形的性质和全等三角形的判定和性质解答即可.
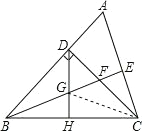
解:连接 CG,
∵BD=DC,H 为 BC 中点,
∴DH 为 BC 垂直平分线,
∴BG=CG,
∴∠ABE=∠CBE=∠GCB,
∵∠ABC=45°,∠ABE=∠CBE,
∴∠EGC=∠CBE+∠GCB=45°,
∵∠GEC=90°,
∴∠ECG=45°=∠EGC,
∴GE=CE=3.
∵BE 平分∠ABC,且 BE⊥AC 于点 E,
∴AE=EC=3,
∴AC=6,
∵CD⊥AB,
∴∠CDB=90°,
∵∠ABC=45°,
∴∠DCB=45°=∠DBC,
∴BD=DC,
在△BDF 和△CEF 中,
∵∠BDC=∠BEC=90°,∠DFB=∠EFC,
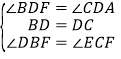 ∴∠DBF=∠ECF, 在△BDF 和△CDA 中
∴∠DBF=∠ECF, 在△BDF 和△CDA 中
∴△BDF≌△CDA(ASA),
∴BF=AC=6; 故答案为:6;


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
查看答案和解析>>
科目:初中数学 来源: 题型:
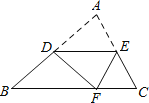
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() 则称
则称![]() 与
与![]() 是关于1的平衡数。
是关于1的平衡数。
(1)5与______是关于1的平衡数;
(2)![]() 与________是关于1的平衡数(用含
与________是关于1的平衡数(用含![]() 的代数式表示);
的代数式表示);
(3)若![]() 判断
判断![]() 与是
与是![]() 否是关于1的平衡数,并说明理由。
否是关于1的平衡数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
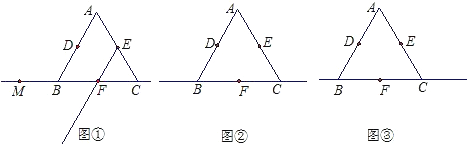
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
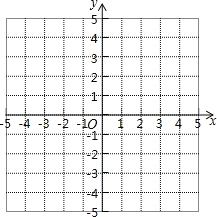
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1) 求出△ABC的面积
(2) 在图形中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1、B1、C1的坐标
(3) 是否存在一点P到AC、AB的距离相等,同时到点A、点B的距离也相等.若存在保留作图痕迹标出点P的位置,并简要说明理由;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
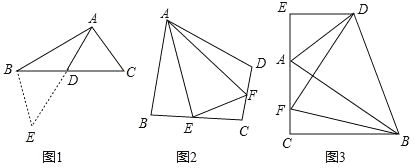
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=![]() AF.
AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)3b﹣2a2﹣(﹣4a+a2+3b)+a2;
(2)﹣13﹣(1﹣![]() )×
)×![]() ×[2﹣(﹣3)2];
×[2﹣(﹣3)2];
(3)﹣|﹣23|+15﹣|4.5﹣(﹣2.5)|;
(4)89′25″﹣48′58″;
(5)化简求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=![]() ,b=
,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
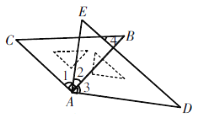
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com