
【题目】定义:若![]() 则称
则称![]() 与
与![]() 是关于1的平衡数。
是关于1的平衡数。
(1)5与______是关于1的平衡数;
(2)![]() 与________是关于1的平衡数(用含
与________是关于1的平衡数(用含![]() 的代数式表示);
的代数式表示);
(3)若![]() 判断
判断![]() 与是
与是![]() 否是关于1的平衡数,并说明理由。
否是关于1的平衡数,并说明理由。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
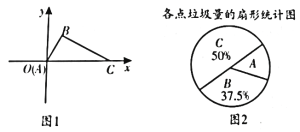
【题目】2017年4月20日,成都举行了“建城市森林,享低碳生活”的垃圾分类推进工作启动仪式,在成都设置有专门的垃圾存放点,做到日产日清。在平面直角坐标系中xOy中,A,B,C三个垃圾存放点的位置如图1所示,点A在原点,![]() ,
,![]() .某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
.某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
(1)若C处的垃圾存放量为320千克,求A处的垃圾存放量。
(2)现需要A,C两处的垃圾分别沿道路AB,CB都运到B处,若点B的横坐标为50,平面直角坐标系中一个单位长度所表示的实际距离是1米,每运送1千克垃圾1米的费用为0.005元,求本次运送垃圾的总费用。(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D,E五个整数点(即各点均表示整数),且AB=2BC=3CD=4DE,若A、E两点表示的数的分别为-13和12,那么,该数轴上上述五个点所表示的整数中,离线段AE的中点最近的整数是( )
![]()
A. -1 B. 5 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
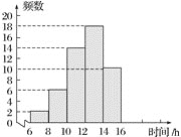
A. 学生参加社会实践活动时间最多的是16 h
B. 学生参加社会实践活动的时间大多数是12~14 h
C. 学生参加社会实践活动时间不少于10 h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6~8 h的大约有26人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题: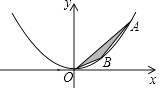
(1)探究:当a=1时,
mn | m﹣n | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m﹣n | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
(2)归纳证明:对任意m、n(m>n>0),猜想S=(用a,m,n表示),并证明你的猜想.
(3)拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=(用a,m,n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
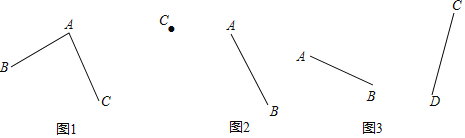
【题目】请按要求完成下面三道小题.
(1)如图1,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请画出对称轴a(尺规作图,保留作图痕迹);如果不是,请说明理由.
(2)如图2,已知线段AB和点C.求作线段CD(不要求尺规作图),使它与AB成轴对称,且A与C是对称点,明对称轴b,并简述画图过程.
(3)如图3,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请描述操作方法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
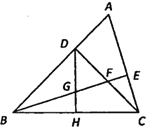
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD 和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )

A. ①② B. ③⑤ C. ①③④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,⊙O的两条弦AB、CD相交于点E,
(1)如图1,若BE=DE,求证: ![]() =
= ![]() ;
; 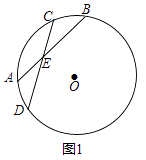
(2)如图2,在(1)的条件下,连接OC,AP为⊙O的直径,PQ为⊙O的弦,且PQ∥AB,求证:∠OCD=∠APQ; 
(3)如图3,在(2)的条件下,连接BD分别与OA、OC交于点G、H,连接DQ,设CD与AP交于点F, 若PQ=2CF,BH=5GH,DQ=4,求⊙O的半径.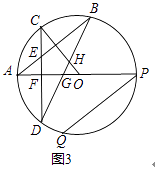
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com