
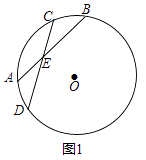
【题目】已知,⊙O的两条弦AB、CD相交于点E,
(1)如图1,若BE=DE,求证: ![]() =
= ![]() ;
; 
(2)如图2,在(1)的条件下,连接OC,AP为⊙O的直径,PQ为⊙O的弦,且PQ∥AB,求证:∠OCD=∠APQ; 
(3)如图3,在(2)的条件下,连接BD分别与OA、OC交于点G、H,连接DQ,设CD与AP交于点F, 若PQ=2CF,BH=5GH,DQ=4,求⊙O的半径.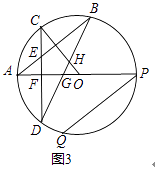
【答案】
(1)证明:连接AD、BC,
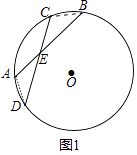
∵ ![]() =
= ![]() ,
,
∴∠B=∠D,
在△AED和△CEB中,
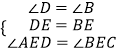 ,
,
∴△AED≌△CEB,
∴AD=BC,
∴ ![]() =
= ![]()
(2)证明:连接AC.
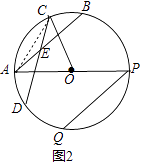
∵ ![]() =
= ![]() ,
,
∴∠BAC=∠ACD,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠BAO=∠OCD,
∵PQ∥AB,
∴∠BAO=∠APQ,
∴∠COD=∠APQ
(3)连接AD、AH、BP、BQ、DP,延长CO交PQ于M,作AN⊥BD于N.
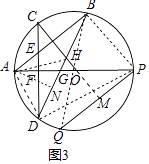
∵∠OCD=∠APQ.OC=OP,∠AOC=∠POM,
∴△COF≌△POM,
∴CF=PM,
∵PQ=2CF,
∴PQ=2PM,
∴M是PQ的中点,
∴OM⊥PQ,
∴∠CFO=∠PMO=90°
∴AP⊥CD,
∴ ![]() =
= ![]() ,
,
PQ∥AB,
∴∠OMP=∠AKM=90°,
∴OC⊥AB,
∴ ![]() =
= ![]() ,
,
∴AK=BK,
∴ ![]() =
= ![]() =
= ![]() ,OC垂直平分AB,设GH=a,
,OC垂直平分AB,设GH=a,
∴BH=5GH=5a,
∵OC垂直平分AB,
∴AH=BH=5a,∠HAB=∠HBA,
∴∠AHD=2∠ABH,
∵ ![]() =
= ![]() =
= ![]() ,
,
∴∠ADC=∠CDB=∠ABD,
∴∠ADH=2∠ADC=2∠ABH=∠AHD,
∴AH=AD=5a,
∵CD⊥AP,
∴∠AFD=∠GFD=90°,
∵DF=DF,∠ADC=∠CDB,
∴△ADF≌△GDF,
∴AD=DG=5a,
∴DH=6a,BD=11a,
∵AH=AD,AN⊥DH,
∴NH= ![]() DH=3a,
DH=3a,
AN= ![]() =4a,BN=BH+NH=8a,
=4a,BN=BH+NH=8a,
在Rt△ABN中,
tan∠ABD= ![]() =
= ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴∠ABD=∠APD,
∴tan∠ABD=tan∠APD= ![]() ,
,
∵AP是直径,
∴∠ADP=90°,
∴ ![]() =
= ![]() ,
,
∴PD=2AD=10a,AP= ![]() =5
=5 ![]() a,
a,
∵AP为直径,
∴∠ABP=90°,
∵PQ∥AB,
∴∠ABP+∠BPQ=180°,
∵∠ABP=90°,
∴∠BPQ=90°,
∴BQ为⊙O的直径,
∴BQ=5 ![]() a,
a,
∵BQ为⊙O的直径,
∴∠BDQ=90°,
∴DQ= ![]() =2a,
=2a,
∵DQ=4,
∴2a=4,
∴a=2,AP=5 ![]() a=10
a=10 ![]() ,
,
∴⊙O的半径OA= ![]() AP=5
AP=5 ![]()
【解析】(1)连接AD、BC,只要证明△AED≌△CEB,即可解决问题.(2)连接AC.想办法证明:∠OCD、∠APQ都与∠PAB相等即可.(3)连接AD、AH、BP、BQ、DP,延长CO交PQ于M,作AN⊥BD于N.由△COF≌△POM,推出M是PQ的中点,OC垂直平分AB,设GH=a,则BH=5GH=5a,由OC垂直平分AB,推出AH=BH=5a,∠HAB=∠HBA,推出∠AHD=2∠ABH,由 ![]() =
= ![]() =
= ![]() ,推出∠ADC=∠CDB=∠ABD,推出∠ADH=2∠ADC=2∠ABH=∠AHD,推出AH=AD=5a,由△ADF≌△GDF,推出AD=DG=5a,推出DH=6a,BD=11a,由AH=AD,AN⊥DH,推出NH=
,推出∠ADC=∠CDB=∠ABD,推出∠ADH=2∠ADC=2∠ABH=∠AHD,推出AH=AD=5a,由△ADF≌△GDF,推出AD=DG=5a,推出DH=6a,BD=11a,由AH=AD,AN⊥DH,推出NH= ![]() DH=3a,AN=
DH=3a,AN= ![]() =4a,BN=BH+NH=8a,在Rt△ABN中, tan∠ABD=
=4a,BN=BH+NH=8a,在Rt△ABN中, tan∠ABD= ![]() =
= ![]() =
= ![]() ,由
,由 ![]() =
= ![]() ,推出∠ABD=∠APD,推出tan∠ABD=tan∠APD=
,推出∠ABD=∠APD,推出tan∠ABD=tan∠APD= ![]() ,推出
,推出 ![]() =
= ![]() ,推出PD=2AD=10a,AP=
,推出PD=2AD=10a,AP= ![]() =5
=5 ![]() a,再证明BQ为⊙O的直径,想办法列出方程即可解决问题.
a,再证明BQ为⊙O的直径,想办法列出方程即可解决问题.


科目:初中数学 来源: 题型:
【题目】定义:若![]() 则称
则称![]() 与
与![]() 是关于1的平衡数。
是关于1的平衡数。
(1)5与______是关于1的平衡数;
(2)![]() 与________是关于1的平衡数(用含
与________是关于1的平衡数(用含![]() 的代数式表示);
的代数式表示);
(3)若![]() 判断
判断![]() 与是
与是![]() 否是关于1的平衡数,并说明理由。
否是关于1的平衡数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)3b﹣2a2﹣(﹣4a+a2+3b)+a2;
(2)﹣13﹣(1﹣![]() )×
)×![]() ×[2﹣(﹣3)2];
×[2﹣(﹣3)2];
(3)﹣|﹣23|+15﹣|4.5﹣(﹣2.5)|;
(4)89′25″﹣48′58″;
(5)化简求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=![]() ,b=
,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知多项式![]() x2ym+1+xy2-2x3+8是六次四项式,单项式-
x2ym+1+xy2-2x3+8是六次四项式,单项式-![]() x3ay5-m的次数与多项式的次数相同,求m,a的值;
x3ay5-m的次数与多项式的次数相同,求m,a的值;
(2)已知多项式mx4+(m-2)x3+(2n+1)x2-3x+n不含x2和x3的项,试写出这个多项式,再求当x=-1时多项式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张明和李强两名运动爱好者周末相约到东湖绿道进行跑步锻炼.(1)周日早上6点,张明和李强同时从家出发,分别骑自行车和步行到离家距离分别为4.5千米和1.2千米的绿道落雁岛入口汇合,结果同时到达,且张明每分钟比李强每分钟多行220米,求张明和李强的速度分别是多少米/分?
(1)两人到达绿道后约定先跑 6 千米再休息,李强的跑步速度是张明跑步速度的m倍,两人在同起点,同时出发,结果李强先到目的地n分钟.
①当m=12,n=5时,求李强跑了多少分钟?
②张明的跑步速度为 米/分(直接用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC,△ADE均为等腰直角三角形,点D,E,C在同一直线上,连接BD.
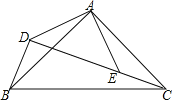
(1)求证:△ADB≌△AEC;
(2)若AD=AE=![]() ,CE=2,求BC的长.
,CE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
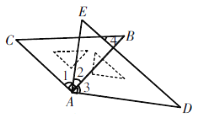
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:等腰△ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
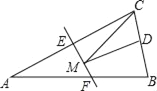
A. 6 B. 8 C. 9 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com