
【题目】如图,等边三角形![]() 的边长为
的边长为![]() ,
,![]() 是
是![]() 边上的高
边上的高![]() 所在的直线,点
所在的直线,点![]() 为直线
为直线![]() 上的一动点,连接
上的一动点,连接![]() 并将
并将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,连接
,连接![]() ,则
,则![]() 的最小值为________.
的最小值为________.

【答案】![]()
【解析】
取AB的中点G,连接DG.先根据条件证明△ADG≌△AEF,从而EF=DG,根据“垂线段最短”可得,当DG⊥AB时,DG最短,再利用勾股定理在Rt△BGD中,求出DG即可.
解:如图,取AB的中点G,连接DG.
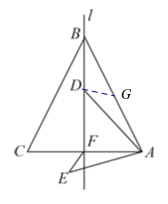
∵旋转角为60°,
∴ ∠DAE=60°,
∵∠BAC=60°,
∴∠GAD=∠BAC -∠DAC=60°-∠DAC,
∠FAE=∠DAE-∠DAF=60°-∠DAC,
∴∠GAD=∠FAE,
∵BF为等边三角形ABC的高,
∴ AF=![]() AC,(等腰三角形三线合一),
AC,(等腰三角形三线合一),
∴AG=AF,
∵AE由AD旋转可得,
∴AD=AE,
在△ADG和△AEF中,
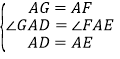 ,
,
∴△ADG≌△AEF,
∴EF=DG,
∴ 当DG⊥AB时,EF最短,
∵∠ABF=![]() ∠ABC=30°,BG=
∠ABC=30°,BG=![]() ×6=3.
×6=3.
∴BD=2DG,(直角三角形中30°角所对的边是斜边的一半),
在Rt△BGD中,
![]() ,
,
∴ 4DG2=DG2+9,
∴ DG=![]() ,
,
∴ EF的最小值为![]() .
.
故答案为:![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD 和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )

A. ①② B. ③⑤ C. ①③④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,⊙O的两条弦AB、CD相交于点E,
(1)如图1,若BE=DE,求证: ![]() =
= ![]() ;
; 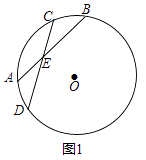
(2)如图2,在(1)的条件下,连接OC,AP为⊙O的直径,PQ为⊙O的弦,且PQ∥AB,求证:∠OCD=∠APQ; 
(3)如图3,在(2)的条件下,连接BD分别与OA、OC交于点G、H,连接DQ,设CD与AP交于点F, 若PQ=2CF,BH=5GH,DQ=4,求⊙O的半径.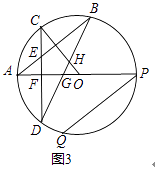
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在哈市地铁一号线施工建设中,安排甲、乙两个工程队完成大连北路至新疆大街路段的铁轨铺设任务,该路段全长3600米.已知甲队每天铺设铁轨的米数是乙队每天铺设铁轨米数的1.5倍,并且甲、乙两队分别单独完成600米长度路段时,甲队比乙队少用10天.
(1)求甲、乙两个工程队每天各能铺设铁轨多少米?
(2)若甲队每天施工的费用为4万元,乙队每天施工的费用为3万元,要使甲、乙两队合作完成大连北路至新疆大街全长3600米的总费用不超过520万元,则至少应安排甲队施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,∠COD=90°,OE、OF分别是∠COB、∠AOD的平分线,且∠COB:∠AOD=4:9.
(1)写出图中∠BOD的余角和补角;
(2)求∠AOC的度数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一根绳子对折成一条线段AB,在线段AB取一点P,使AP=![]() ,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
,从P处把绳子剪断,若剪断后的三段绳子中最长的一段为30cm,则绳子的原长为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
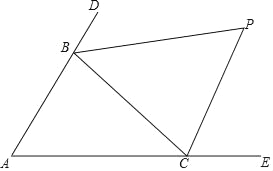
【题目】如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com