
【题目】如图,O是直线AB上一点,∠COD=90°,OE、OF分别是∠COB、∠AOD的平分线,且∠COB:∠AOD=4:9.
(1)写出图中∠BOD的余角和补角;
(2)求∠AOC的度数

【答案】(1)∠BOD的余角为∠BOC,∠BOD的补角为∠AOD;(2)∠AOC=108°.
【解析】
(1)依据∠COD=90°,∠AOB=180°,即可得到∠BOD的余角为∠BOC,∠BOD的补角为∠AOD;
(2)依据∠COB:∠AOD=4:9,即可得到9(90°﹣∠BOD)=4(180°﹣∠BOD),求得∠BOD=18°,即可得到∠AOC的度数.
解:(1)∵∠COD=90°,∠AOB=180°,
∴∠BOC=90°﹣∠BOD,∠AOD=180°﹣∠BOD,
即∠BOD的余角为∠BOC,∠BOD的补角为∠AOD;
(2)∵∠COB:∠AOD=4:9,且∠BOC=90°﹣∠BOD,∠AOD=180°﹣∠BOD,
∴9(90°﹣∠BOD)=4(180°﹣∠BOD),
解得∠BOD=18°,
∴∠BOC=90°﹣18°=72°,
∴∠AOC=180°﹣72°=108°.


科目:初中数学 来源: 题型:
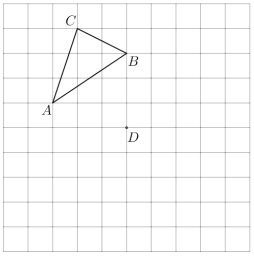
【题目】在图中网格上按要求画出图形,并回答问题:
(1)如果将三角形![]() 平移,使得点
平移,使得点![]() 平移到图中点
平移到图中点![]() 位置,点
位置,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,请画出三角形
,请画出三角形![]() ;
;
(2)画出三角形![]() 关于点
关于点![]() 成中心对称的三角形
成中心对称的三角形![]() .
.
(3)三角形![]() 与三角形
与三角形![]() 是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点
是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC,△ADE均为等腰直角三角形,点D,E,C在同一直线上,连接BD.
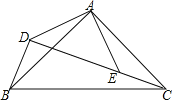
(1)求证:△ADB≌△AEC;
(2)若AD=AE=![]() ,CE=2,求BC的长.
,CE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
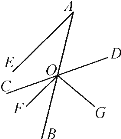
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于点O,AE∥OF,且∠A=30°.
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线a∥b,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,
,![]() .点
.点![]() 、
、![]() 从
从![]() 点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动
点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动![]() 秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)
秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)
(1)当![]() 秒时,点
秒时,点![]() 到直线
到直线![]() 的距离为 ;
的距离为 ;
(2)若△ACD是直角三角形,t的值为 ;
(3)若△ACD是等腰三角形,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了准备“迎新活动”,用700元购买了甲、乙两种小礼品260个,其中购买甲种礼品比乙种礼品少用了100元.
(1)购买乙种礼品花了______元;
(2)如果甲种礼品的单价比乙种礼品的单价高20%,求乙种礼品的单价.(列分式方程解应用题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com