
����Ŀ���ڹ��е���һ����ʩ�������У����żס����������̶���ɴ�����·���½����·�ε�������������·��ȫ��3600�ף���֪��ÿ������������������Ҷ�ÿ����������������1.5�������Ҽס������ӷֱ����600�׳���·��ʱ���ӱ��Ҷ�����10�죮
��1����ס����������̶�ÿ�����������������ף�
��2������ÿ��ʩ���ķ���Ϊ4��Ԫ���Ҷ�ÿ��ʩ���ķ���Ϊ3��Ԫ��Ҫʹ�ס������Ӻ�����ɴ�����·���½����ȫ��3600���ܷ��ò�����520��Ԫ��������Ӧ���ż�ʩ�������죿
���𰸡�
��1���⣺���ҹ��̶�ÿ����������x�ף�
�������� �� ![]() ��
�� ![]() =10��
=10��
���x=20��
������x=20��
��ԭ���̵Ľ⣮
����1.5x=1.5��20=30
�𣺼��̶�ÿ����������30�ף��ҹ��̶�ÿ����������20�ף�
��2���⣺�谲�ż�ʩ��a��
4a+ ![]() ��3��520��
��3��520��
���a��40��
�����ٰ��ż�ʩ��40�죮
������������1�����ҹ��̶�ÿ�����賤��Ϊx�ף�����̶�ÿ�������ij���Ϊ1.5x�ף���������600��·����̶ӱ��ҹ��̶�����10�죬�з�����⣻��2���谲�ż��̶�ʩ��a�죬���ݼס������Ӻ�����ɴ�����·���½����ȫ��3600���ܷ��ò�����520��Ԫ���в���ʽ��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�Ȼ�������⣺�͡�������ֵ����������Ź㷺��Ӧ�ã��س����벹�̷���֤���߶εĺ͡�������ֵ����������Ź㷺��Ӧ�ã��������������ij���߶��Ͻ�ȡһ���߶ε���ij�ض��߶Σ���ij���߶��ӳ���ʹ֮��ij�ض��߶���ȣ�������ȫ�������ε����ʵ��й�֪ʶ�������ѧ���⣮
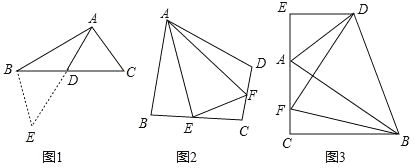
��1����ͼ1������ABC�У��� AB��12��AC��8���� BC���ϵ�����AD��ȡֵ��Χ��
�����������������·������ӳ�AD����Eʹ DE��AD�������� BE����AB��AC��2AD��������ABE�У��������������ߵĹ�ϵ�����ж����� AD��ȡֵ��Χ��_______.
��������
��2����ͼ2�����ı���ABCD�У�AB��AD����ABC+��ADC��180�㣬E��F�ֱ��DZ�BC��CD�ϵ����㣬����EAF��![]() ��BAD����֤��BE+DF��EF��
��BAD����֤��BE+DF��EF��
������չ��
��3����ͼ3������ABC�У���ACB��90�㣬��CAB��60������D����ABC ���ƽ������һ�㣬DE��AC�� CA�ӳ����ڵ�E��F�� AC��һ�㣬��DF��DB��
��֤��AC��AE��![]() AF��
AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ǿ�����˶���������ĩ��Լ�������̵������ܲ���������1����������6�㣬��������ǿͬʱ�Ӽҳ������ֱ������г��Ͳ��е���Ҿ���ֱ�Ϊ4.5ǧ��1.2ǧ���̵����㵺��ڻ�ϣ����ͬʱ���������ÿ���ӱ���ǿÿ���Ӷ���220�ף�����������ǿ���ٶȷֱ��Ƕ�����/�֣�
��1�����˵����̵���Լ������ 6 ǧ������Ϣ����ǿ���ܲ��ٶ��������ܲ��ٶȵ�m����������ͬ��㣬ͬʱ�����������ǿ�ȵ�Ŀ�ĵ�n���ӣ�
�ٵ�m��12��n��5ʱ������ǿ���˶��ٷ��ӣ�
���������ܲ��ٶ�Ϊ ��/�֣�ֱ���ú�m��n��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ尴��ͼ���ã������н�����
�������2=30�㣬����AC��DE��
�ڡ�BAE+��CAD =180�㣻
�����BC��AD�����С�2=45�㣻
�������CAD=150��������4=��C��
��ȷ����( )
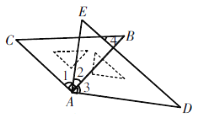
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����š������У���������ƽ���ȫ����Сѧ�������������ձ���ǿ��ijУΪ��ȷ����ѧ���ڡ������У�����չ��������������ȫУѧ���������ȡ����ѧ�������������ʲ��ԣ����ԵĽ����ΪA��B��C��D��E����ȼ�����������������������ͳ��ͼ�������ͳ��ͼ����Ϣ�ش��������⣺ 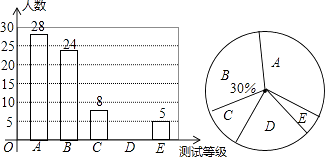
��1�����γ����������ȡ��ѧ�������ˣ�
��2���ڱ��α������ѧ���У�����Խ��ΪD�ȼ���ѧ������������ȫ����ͳ��ͼ��
��3������ѧУ����ѧ��1200�ˣ�������ݳ�������Ľ�����Ƹ�ѧУȫ��ѧ�����������ʲ��Խ��ΪA�ȼ���ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ��
��![]() ��
��![]() ���ϵĸ�
���ϵĸ�![]() ���ڵ�ֱ�ߣ���
���ڵ�ֱ�ߣ���![]() Ϊֱ��
Ϊֱ��![]() �ϵ�һ���㣬����
�ϵ�һ���㣬����![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��
��![]() ������
������![]() ����
����![]() ����СֵΪ________��
����СֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɫ���У���̼�������ѳ�Ϊ�������Ĺ�ʶ��Ϊ����������У���̨���Ƴ��˹������г�ϵͳ���շ���СʱΪ��λ��ÿ��ʹ�ò�����1Сʱ����ѣ�����1Сʱ����1Сʱ�IJ��ְ�1Сʱ�շѣ�С��ͬѧͨ�������֪�����г�ʹ��ʱ��Ϊ3Сʱ���շ�2Ԫ��ʹ��ʱ��Ϊ4Сʱ���շ�3Ԫ�������ֵ�ʹ��ʱ�䳬��1Сʱ���ó�������ʹ��ʱ��֮�����һ�κ����Ĺ�ϵ��
��1����ʹ�����г��ķ���Ϊ![]() Ԫ��ʹ��ʱ��Ϊ
Ԫ��ʹ��ʱ��Ϊ![]() Сʱ��
Сʱ��![]() Ϊ����1������������
����1������������![]() ��
��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����С��˴�ʹ�ù������г�5Сʱ������Ӧ������Ԫ���ã�
��3����С��˴�ʹ�ù������г�����6Ԫ��������ʹ�����г���ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
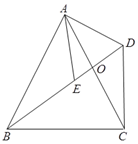
����Ŀ����ͼ���ı���ABCD�У��Խ���AC��BD���ڵ�O��AB��AC����E��BD��һ�㣬��AE��AD����EAD����BAC��
�� ��֤����ABD����ACD��
�� ����ACB��65�㣬���BDC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��AD��BC��CE��AB��AE=CE����֤��

��1����AEF�ա�CEB��
��2��AF=2CD��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com