
����Ŀ���Ķ����в��ϣ�Ȼ�������⣺�͡�������ֵ����������Ź㷺��Ӧ�ã��س����벹�̷���֤���߶εĺ͡�������ֵ����������Ź㷺��Ӧ�ã��������������ij���߶��Ͻ�ȡһ���߶ε���ij�ض��߶Σ���ij���߶��ӳ���ʹ֮��ij�ض��߶���ȣ�������ȫ�������ε����ʵ��й�֪ʶ�������ѧ���⣮
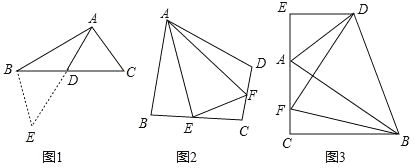
��1����ͼ1������ABC�У��� AB��12��AC��8���� BC���ϵ�����AD��ȡֵ��Χ��
�����������������·������ӳ�AD����Eʹ DE��AD�������� BE����AB��AC��2AD��������ABE�У��������������ߵĹ�ϵ�����ж����� AD��ȡֵ��Χ��_______.
��������
��2����ͼ2�����ı���ABCD�У�AB��AD����ABC+��ADC��180�㣬E��F�ֱ��DZ�BC��CD�ϵ����㣬����EAF��![]() ��BAD����֤��BE+DF��EF��
��BAD����֤��BE+DF��EF��
������չ��
��3����ͼ3������ABC�У���ACB��90�㣬��CAB��60������D����ABC ���ƽ������һ�㣬DE��AC�� CA�ӳ����ڵ�E��F�� AC��һ�㣬��DF��DB��
��֤��AC��AE��![]() AF��
AF��
���𰸡���1��2��AD��10����2��֤������������3��֤��������.
��������
��1���ӳ� AD ���� E ʹ DE��AD������ BE��֤����ADC�ա�EDB������ȫ�������ε����ʵõ� BE��AC���������������߹�ϵ���㣻
��2���ӳ� CB �� G��ʹ BG��DF��֤����ABG�ա�ADF������ȫ�������ε����ʵõ� AG��AF����GAB����FAD��֤����AEG�ա�AEF������ȫ�������ε�����֤����
��3���� DH��AB �� H���� AB �Ͻ�ȡ BR��AF���ֱ�֤�� Rt��DEF��Rt��DHB��
 ��DAF�ա�DRB������ȫ�������ε�����֤����
��DAF�ա�DRB������ȫ�������ε�����֤����
�⣺��1���ӳ� AD ����Eʹ DE��AD������ BE��
����ADC ����EDB��

���ADC�ա�EDB��SAS����
��BE��AC��8��
AB��BE��AE��AB+BE����21��8��2AD��12+8��
��2��AD��10��
�ʴ�Ϊ��2��AD��10��
��2��֤�����ӳ� CB �� G��ʹ BG��DF��
�ߡ�ABC+��ADC��180�㣬��ABC+��ABG��180�㣬
���ADC����ABG��
����ABG ����ADF ��

���ABG�ա�ADF��SAS����
��AG��AF����GAB����FAD��
�ߡ�EAF�� ![]() ��BAD��
��BAD��
���FAD+��BAE����GAB+��BAE��![]() ��BAD��
��BAD��
���GAE����FAE��
����AEG ����AEF ��

���AEG�ա�AEF��SAS����
��EF��GE��
��EF��BE+BG��BE+DF��

��3��֤������ DH��AB �� H���� AB �Ͻ�ȡ BR��AF��
�ߡ�CAB��60�㣬��ACB��90�㣬
���ABC��30�㣬
��AB��2AC��
�ߵ� D ����ABC ���ƽ������һ�㣬DE��AC��DH��AB��
��DE��DH��AH��AE��
�� Rt��DEF �� Rt��DHB ��
![]()
��Rt��DEF��Rt��DHB��HL��
���DFA����DBA��
����DAF ����DRB ��

���DAF�ա�DRB��SAS��
��DA��DR��
��AH��HR��AE�� ![]() AR��
AR��
��AF��BR��AB��AR��2AC��2AE
��AC��AE��![]() AF��
AF��


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������˾��һ��סլ¥�ı���ǣ�����2580Ԫ/ƽ���ף�¥�������±���

�����������Ϊ80ƽ������¥��
��1�����������˶���Ǯ��
��2��������ͬ�����Ǯȥ����¥�������������һ�������Զ������ƽ���ķ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龰��
��ͼ����ֱ������ϵxOy�У���A��BΪ���κ���y=ax2��a��0��ͼ���ϵ����㣬�ҵ�A��B�ĺ�����ֱ�Ϊm��n��m��n��0��������OA��AB��OB�����AOB�����ΪSʱ������������⣺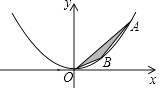
��1��̽������a=1ʱ��
mn | m��n | S | |
m=3��n=1 | 3 | 2 | |
m=5��n=2 | 10 | 3 |
��a=2ʱ��
2mn | m��n | S | |
m=3��n=1 | 6 | 2 | |
m=5��n=2 | 20 | 3 |
��2������֤����������m��n��m��n��0��������S=����a��m��n��ʾ������֤����IJ��룮
��3����չӦ�ã�
����A��B�ĺ�����ֱ�Ϊm��n��m��0��n����������������ʱ����AOB�����S=����a��m��n��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC��45�㣬CD��AB�ڵ�D��BEƽ�֡�ABC����BE��AC�ڵ�E����CD�ཻ�ڵ�F��H�DZ�BC���е㣬���� DH�� BE�ཻ�ڵ� G����GE��3����BF��_____��
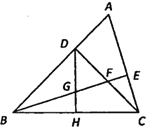
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
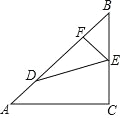
����Ŀ����ͼ����ABC�У�AC��BC����ACB��90������ D��E�ֱ���AB��BC�ϣ���AD��BE��BD��AC����E��EF��AB��F��
��1����֤����FED����CED��
��2���� BF��![]() ��ֱ��д�� CE�ij�Ϊ_______��
��ֱ��д�� CE�ij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�����ߣ�E��F�ֱ���AD��AD�ӳ����ϵĵ㣬��DE��DF������BF��CE������˵�����١�ABD �͡�ACD�����ȣ��ڡ�BAD����CAD���ۡ�BDF�ա�CDE����BF��CE����CE��AE��������ȷ���ǣ� ��

A. �٢� B. �ۢ� C. �٢ۢ� D. �٢ܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������������ǽڼ���������ȵ㾰����ijѧУ�Ծţ�1����ѧ������һ��С�����游ĸ����������������ļƻ�����ȫ����飬������ĸ����A������������B��������������C����һ��������D�������������������棬�ָ��ݵ����������˲���ȫ������ͳ��ͼ������ͳ��ͼ���£� 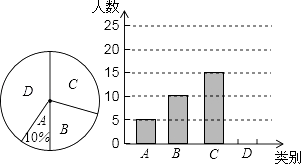
����ͼ����Ϣ����������⣺
��1���ţ�1��������ѧ���ˣ�������ͳ��ͼ�б�ʾ��B��𡱵����ε�Բ�ĽǵĶ���Ϊ��
��2���뽫����ͳ��ͼ����������
��3������У���꼶��1000��ѧ������ƻ�����һ��С�����游ĸ�����������������ѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC�ı߳�Ϊ 1��CD��AB �ڵ� D��E Ϊ���� CD ��һ�㣬��BEΪ���� BE ������ȱߡ�BEF����DF����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڹ��е���һ����ʩ�������У����żס����������̶���ɴ�����·���½����·�ε�������������·��ȫ��3600�ף���֪��ÿ������������������Ҷ�ÿ����������������1.5�������Ҽס������ӷֱ����600�׳���·��ʱ���ӱ��Ҷ�����10�죮
��1����ס����������̶�ÿ�����������������ף�
��2������ÿ��ʩ���ķ���Ϊ4��Ԫ���Ҷ�ÿ��ʩ���ķ���Ϊ3��Ԫ��Ҫʹ�ס������Ӻ�����ɴ�����·���½����ȫ��3600���ܷ��ò�����520��Ԫ��������Ӧ���ż�ʩ�������죿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com