
【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题: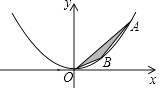
(1)探究:当a=1时,
mn | m﹣n | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m﹣n | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
(2)归纳证明:对任意m、n(m>n>0),猜想S=(用a,m,n表示),并证明你的猜想.
(3)拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=(用a,m,n表示).
【答案】
(1)3;15;6;30;
(2)![]()
amn(m﹣n)
(3)![]()
amn(m﹣n)
【解析】(1.)解:探究:
如图1,设直线AB交y轴于点C,过点A作AD⊥y轴于点D,过B作BE⊥y轴于点E,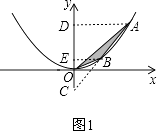
当a=1时,
∵A、B在抛物线上,
∴A(m,m2),B(n,n2),
∴AD=m,BE=n,
设直线AB解析式为y=kx+b,
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线AB解析式为y=(m+n)x﹣mn,
令x=0可得y=﹣mn,
∴OC=mn,
∴S△AOB=S△OCA﹣S△OCB= ![]() OCAD﹣
OCAD﹣ ![]() OCBE=
OCBE= ![]() OC(AD﹣BE)=
OC(AD﹣BE)= ![]() mn(m﹣n),
mn(m﹣n),
当m=3,n=1时,可得S= ![]() ×3×2=3,
×3×2=3,
当m=5,n=2时,可得S= ![]() ×10×3=15;
×10×3=15;
同理可得当a=2时,S= ![]() ×2mn(m﹣n)=mn(m﹣n),
×2mn(m﹣n)=mn(m﹣n),
当m=3,n=1时,S= ![]() ×6×2=6,
×6×2=6,
当m=5,n=2时,S= ![]() ×20×3=30;
×20×3=30;
所以答案是:3;15;6;30;
(2.)归纳证明:可猜想S= ![]() amn(m﹣n).
amn(m﹣n).
证明如下:同图1,
∵A、B在抛物线上,
∴A(m,am2),B(n,an2),
∴AD=m,BE=n,
设直线AB解析式为y=kx+b,
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线AB解析式为y=a(m+n)x﹣amn,
令x=0可得y=﹣amn,
∴OC=amn,
∴S△AOB=S△OCA﹣S△OCB= ![]() OCAD﹣
OCAD﹣ ![]() OCBE=
OCBE= ![]() OC(AD﹣BE)=
OC(AD﹣BE)= ![]() amn(m﹣n);
amn(m﹣n);
所以答案是: ![]() amn(m﹣n);
amn(m﹣n);
(3.)解:拓展应用:
如图2,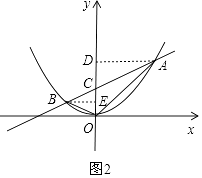
同(2)可得S=S△AOB=S△OCA+S△OCB= ![]() amn[m+(﹣n)]=
amn[m+(﹣n)]= ![]() amn(m﹣n),
amn(m﹣n),
所以答案是: ![]() amn(m﹣n).
amn(m﹣n).


科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(0,6)的抛物线y= ![]() x2+bx+c与x轴相交于B(﹣2,0)、C两点.
x2+bx+c与x轴相交于B(﹣2,0)、C两点.
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)求直线AC所对应的函数关系式;
(3)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1 , 若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(4)在(3)的结论下,新抛物线y1上是否存在点Q,使得△QAB是以AB为底边的等腰三角形,请分析所有可能出现的情况,并直接写出相对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.

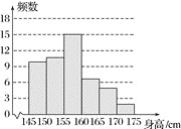
(1)表中m=________,n=________;
(2)身高x满足160≤x<170的校服记为L号,则需要订购L号校服的学生占被调查学生的百分数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() 则称
则称![]() 与
与![]() 是关于1的平衡数。
是关于1的平衡数。
(1)5与______是关于1的平衡数;
(2)![]() 与________是关于1的平衡数(用含
与________是关于1的平衡数(用含![]() 的代数式表示);
的代数式表示);
(3)若![]() 判断
判断![]() 与是
与是![]() 否是关于1的平衡数,并说明理由。
否是关于1的平衡数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
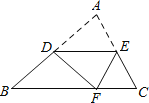
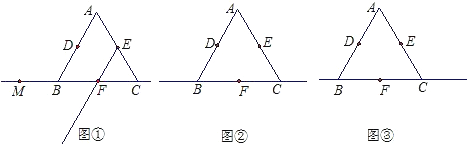
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
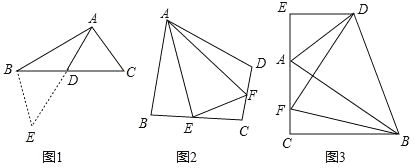
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=![]() AF.
AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张明和李强两名运动爱好者周末相约到东湖绿道进行跑步锻炼.(1)周日早上6点,张明和李强同时从家出发,分别骑自行车和步行到离家距离分别为4.5千米和1.2千米的绿道落雁岛入口汇合,结果同时到达,且张明每分钟比李强每分钟多行220米,求张明和李强的速度分别是多少米/分?
(1)两人到达绿道后约定先跑 6 千米再休息,李强的跑步速度是张明跑步速度的m倍,两人在同起点,同时出发,结果李强先到目的地n分钟.
①当m=12,n=5时,求李强跑了多少分钟?
②张明的跑步速度为 米/分(直接用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com