
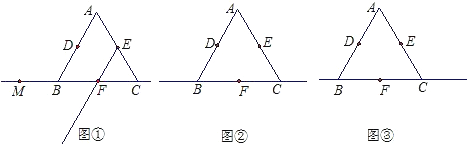
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
【答案】(1)图详见解析,△DMN是等边三角形;(2)△DMN仍是等边三角形,证明详见解析;(3)△DMN不是等边三角形.
【解析】
(1)连接DF,根据等边三角形的性质与三角形中位线平行于第三边并且等于第三边的一半的性质可以证明DF=BD=EF=BF,然后证明BM=FN,∠MBD=∠NFD=120°,从而证明△BDM与△FDN全等,根据全等三角形对应边相等可得MD=DN,对应角相等可得∠MDB=∠NDF,然后证明∠MDN=∠BDF=60°,所以△DMN是等边三角形;(2)连接DF,根据等边三角形的性质与三角形中位线平行于第三边并且等于第三边的一半的性质可以证明DF=BD=EF=BF,然后证明BM=FN,∠MBD=∠NFD=60°,从而证明△BDM与△FDN全等,根据全等三角形对应边相等可得MD=DN,对应角相等可得∠MDB=∠NDF,然后证明∠MDN=∠BDF=60°,所以△DMN是等边三角形; (3)沿用前两问的思路,显然不能证明△CDM与△FDN全等,所以△DMN不是等边三角形.
解:(1)如图①,
△DMN是等边三角形.
(2)如图②,当M在线段BF上(与点B、F重合)时,△DMN仍是等边三角形.
证明:连接DF,
∵△ABC是等边三角形,
∴∠ABC=60°,AB=AC=BC.
∵D、E、F分别是△ABC三边的中点,
∴DE、DF、EF是等边三角形的中位线.
∴DF=![]() AC,BD=
AC,BD=![]() AB,EF=
AB,EF=![]() AB,BF=
AB,BF=![]() BC.
BC.
∴∠BDF=∠A=∠DFE=60°,DF=BF=EF,
∴∠ABC=∠DFE,
∵FM=EN,
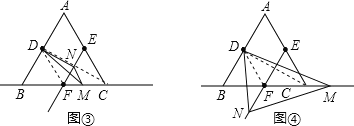
∴BM=NF,
∴△BDM≌△FDN,
∴∠BDM=∠FDN,MD=ND,
∴∠BDM+∠MDF=∠FDN+∠MDF=∠MDN=60°,
△DMN是等边三角形;
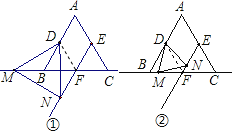
(3)如图③或图④,当点M在射线FC上(与点F不重合)时,(1)中的结论不成立,
即△DMN不是等边三角形.


科目:初中数学 来源: 题型:
【题目】林华在2018年共两次到某商场按照标价购买了A,B两种商品,其购买情况如下表:
购买A商品的数量(个) | 购买B商品的数量(个) | 购买两种商品的总费用(元) | |
第一次购买 | 6 | 5 | 1140 |
第二次购买 | 3 | 7 | 1110 |
(1)分别求出A、B两种商品的标价。
(2)最近商场实行“迎2019新春”的促销活动,A,B两种商品都打折且折扣数相同,于是林华前往商场花1062元又购买了9个A商品和8个B商品,试问本次促销活动中A,B商品的折扣数都为多少?在本次购买中,林华共节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3) 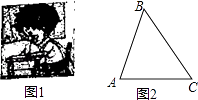
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题: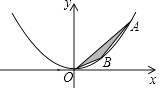
(1)探究:当a=1时,
mn | m﹣n | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m﹣n | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
(2)归纳证明:对任意m、n(m>n>0),猜想S=(用a,m,n表示),并证明你的猜想.
(3)拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=(用a,m,n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
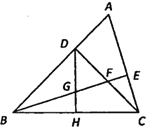
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点 D,E分别在AB,BC上,且AD=BE,BD=AC,过E作EF⊥AB于F.
(1)求证:∠FED=∠CED;
(2)若 BF=![]() ,直接写出 CE的长为_______.
,直接写出 CE的长为_______.
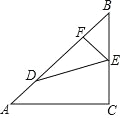
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下: 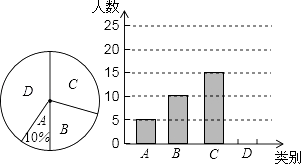
请结合图中信息解答下列问题:
(1)九(1)班现有学生人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.

(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com