
【题目】如图,在矩形ABCD中,E为边AB的中点,将△CBE沿CE翻折得到△CFE,连接AF.若∠EAF=70°,那么∠BCF=度. 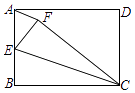
【答案】40
【解析】解:∵四边形ABCD是矩形, ∴∠B=90°,
∵E为边AB的中点,
∴AE=BE,
由折叠的性质可得:∠EFC=∠B=90°,∠FEC=∠CEB,∠FCE=∠BCE,FE=BE,
∴AE=FE,
∴∠EFA=∠EAF=70°,
∴∠BEF=∠EAF+∠EFA=140°,
∴∠CEB=∠FEC=70°,
∴∠FCE=∠BCE=90°﹣70°=20°,
∴∠BCF=20°+20°=40°;
所以答案是:40.
【考点精析】掌握矩形的性质和翻折变换(折叠问题)是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在△ABC的内部且DB=DC,点E,F在△ABC的外部,FB=FA,EA=EC,∠FBA=∠DBC=∠ECA.
(1)①填空:△ACE∽∽;
(2)求证:△CDE∽△CBA;
(3)求证:△FBD≌△EDC;
(4)若点D在∠BAC的平分线上,判断四边形AFDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.

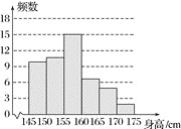
(1)表中m=________,n=________;
(2)身高x满足160≤x<170的校服记为L号,则需要订购L号校服的学生占被调查学生的百分数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.
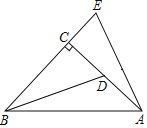
查看答案和解析>>
科目:初中数学 来源: 题型:
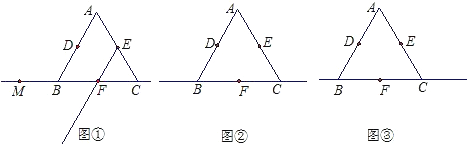
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的边AD与经过A、B、C三点的⊙O相切 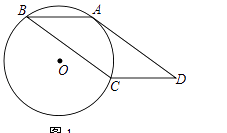
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E= ![]() ,求tan∠D
,求tan∠D 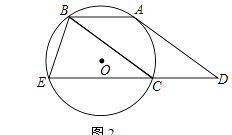
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是G,且点G在边AD上,若EG⊥AC,AB=2,则FG的长为 . 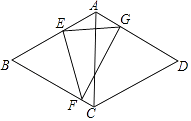
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线 AB 分别交 x 轴、y 轴于点A(a,0)点 B(0,b),且a、b满足a2+4a+4+|2a+b|=0
(1)a= ;b= .
(2)点 P 在直线AB的右侧,且∠APB=45°
①若点P在x轴上,则点P的坐标为 ;
②若△ABP 为直角三角形,求点P的坐标;
(2)如图2,在(2)的条件下,点P在第四象限,∠BAP=90°,AP与y轴交于点M,BP与x轴交于点N,连接MN,求证:MP平分△BMN的一个外角.
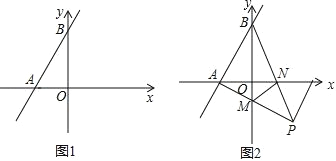
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com