
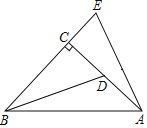
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.
科目:初中数学 来源: 题型:
【题目】七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
七(3)班“绿色奥运”知识竞赛成绩频数统计表
分数段/分 | 组中值/分 | 频数/人 | 频率 |
49.5~59.5 | 54.5 | a | 0.050 |
59.5~69.5 | 64.5 | 9 | 0.225 |
69.5~79.5 | 74.5 | 10 | 0.250 |
79.5~89.5 | 84.5 | 14 | 0.350 |
89.5~99.5 | 94.5 | 5 | b |
七(3)班“绿色奥运”知识竞赛成绩频数直方图
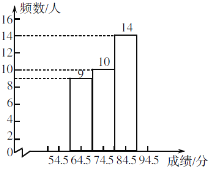
(1)频数统计表中a=_____,b=______;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE. 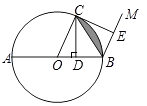
(1)当∠COB=60°时,直接写出阴影部分的面积;
(2)求证:CE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题 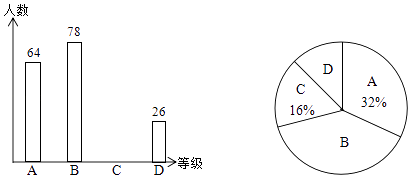
(1)在这次抽样调查中,一共抽取了名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y= ![]() x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点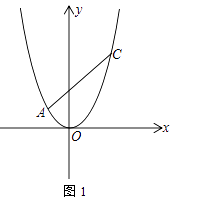
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.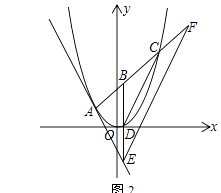
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至G,使CG=BF,连接CE、DE、DG.
(1)如图1,求证:四边形CEDG是平行四边形 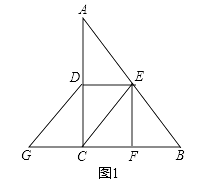 ;
;
(2)如图2,连接EG交AC于点H,若EG⊥AB,请直接写出图2中所有长度等于 ![]() GH的线段.
GH的线段. 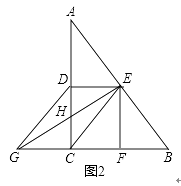
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com