
【题目】在平面直角坐标系中,抛物线y= ![]() x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点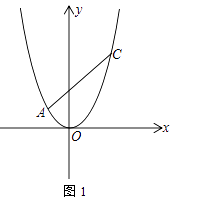
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.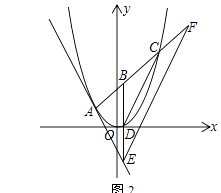
【答案】
(1)
解:∵x1、x2是方程x2﹣2x﹣8的两根,且x1<x2,
∴x1=﹣2,x2=4,
∴A(﹣2,2),C(4,8);
(2)
解:设直线l的解析式为y=kx+b,
∵A(﹣2,2)在直线l上,
∴2=﹣2k+b,
∴b=2k+2,
∴直线l的解析式为y=kx+2k+2①,
∵抛物线y= ![]() x2②,
x2②,
联立①②化简得,x2﹣2kx﹣4k﹣4=0,
∵直线l与抛物线只有一个公共点,
∴△=(2k)2﹣4(﹣4k﹣4)=4k2+16k+16=4(k2+4k+4)=4(k+2)2=0,
∴k=﹣2,
∴b=2k+2=﹣2,
∴直线l的解析式为y=﹣2x﹣2;
(3)
解:由(1)知,A(﹣2,2),C(4,8),
∴直线AC的解析式为y=x+4,
设点B(m,m+4),
∵(4.8),
∴BC= ![]() |m﹣4|=
|m﹣4|= ![]() (4﹣m)
(4﹣m)
∵过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,
∴D(m, ![]() m2),E(m,﹣2m﹣2),
m2),E(m,﹣2m﹣2),
∴BD=m+4﹣ ![]() m2,BE=m+4﹣(﹣2m﹣2)=3m+6,
m2,BE=m+4﹣(﹣2m﹣2)=3m+6,
∵DC∥EF,
∴△BDC∽△BEF,
∴ ![]() ,
,
∴ ![]() ,
,
∴BF=6 ![]() .
.
【解析】(1)解一元二次方程即可得出点A,C坐标;(2)先设出直线l的解析式,再联立抛物线解析式,用△=0,求出k的值,即可得出直线l的解析式;(3)设出点B的坐标,进而求出BC,再表示出点D,E的坐标,进而得出BD,BE,再判断出△BDC∽△BEF得出比例式建立方程即可求出BF.


科目:初中数学 来源: 题型:
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象. 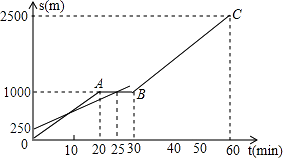
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.
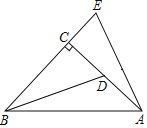
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的边AD与经过A、B、C三点的⊙O相切 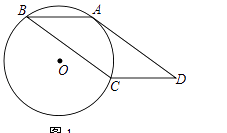
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E= ![]() ,求tan∠D
,求tan∠D 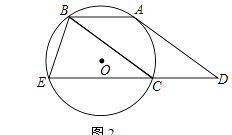
查看答案和解析>>
科目:初中数学 来源: 题型:
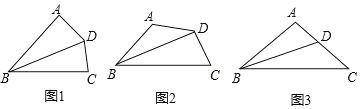
【题目】如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是__________.
(2)问题解决:如图,求证AD=CD;
(3)问题拓展:如图,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是G,且点G在边AD上,若EG⊥AC,AB=2,则FG的长为 . 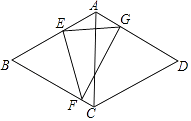
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点 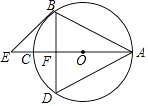
(1)求证:BE为⊙O的切线;
(2)若AF=4CF,求tan∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A(﹣4,0)、B(6,0)两点,与y轴交于点C.
x2+bx+c与x轴交于点A(﹣4,0)、B(6,0)两点,与y轴交于点C.
(1)如图l,求抛物线的解析式;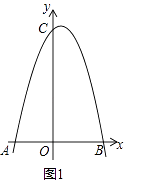
(2)如图2,点P为第一象限抛物线上一点,连接PC、PA,PA交y轴于点F,设点P的横坐标为t,△CPF的面积为S.求S与t的函数关系式(不要求写出自变量t的取值范围);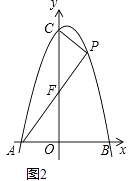
(3)如图3,在(2)的条件下,连接BC,过点P作PD∥y轴变BC于点D,点H为AF中点,且点N(0,1),连接NH、BH,将∠NHB绕点H逆时针旋转,使角的一条边H落在射线HF上,另一条边HN变抛物线于点Q,当BH=BD时,求点Q坐标.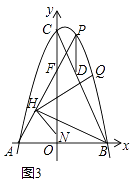
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com