
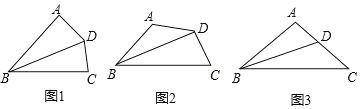
【题目】如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是__________.
(2)问题解决:如图,求证AD=CD;
(3)问题拓展:如图,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
【答案】(1)角平分线上的点到角的两边距离相等;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据角平分线的性质定理解答;
(2)作 DE⊥BA 交 BA 延长线于 E,DF⊥BC 于 F,证明△DEA≌△DFC,根据全等三角形的性质证明;
(3)在 BC 时截取 BK=BD,连接 DK,根据(2)的结论得到 AD=DK,根据等腰三角形的判定定理得到 KD=KC,结合图形证明.
解:(1)∵BD 平分∠ABC,∠BAD=90°,∠BCD=90°,
∴DA=DC(角平分线上的点到角的两边距离相等),
故答案为:角平分线上的点到角的两边距离相等;
(2)如图 2,作DE⊥BA 交 BA延长线于 E,DF⊥BC 于 F,
∵BD 平分∠EBF,DE⊥BE,DF⊥BF,
∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C,
在△DEA 和△DFC 中,
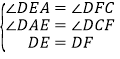
∴△DEA≌△DFC(AAS),
∴DA=DC;
(3)如图,在 BC 时截取 BK=BD,连接 DK,
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°,
∵BD 平分∠ABC,
∴∠DBK=![]() ∠ABC=20°,
∠ABC=20°,
∵BD=BK,
∴∠BKD=∠BDK=80°,即∠A+∠BKD=80°, 由(2)的结论得 AD=DK,
∵∠BKD=∠C+∠KDC,
∴∠KDC=∠C=40°,
∴DK=CK,
∴AD=DK=CK,
∴BD+AD=BK+CK=BC.


科目:初中数学 来源: 题型:
【题目】海静中学开展以“我最喜爱的职业”为主题的调查活动,围绕“在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题: 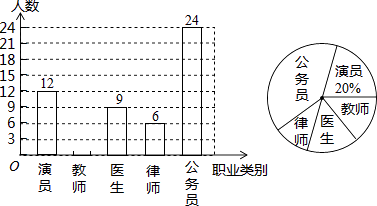
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;
(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE. 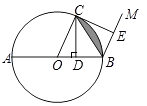
(1)当∠COB=60°时,直接写出阴影部分的面积;
(2)求证:CE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题 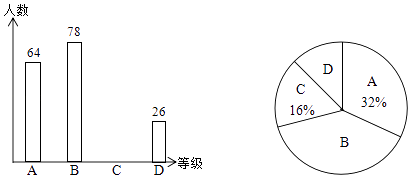
(1)在这次抽样调查中,一共抽取了名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y= ![]() x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点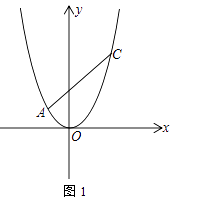
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.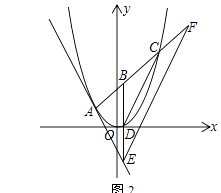
查看答案和解析>>
科目:初中数学 来源: 题型:
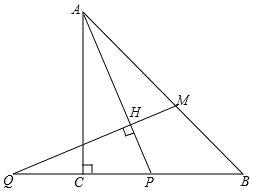
【题目】如图,在等腰Rt△ABC中,角ACB=90°,P是线段BC上一动点(与点B,C不重合)连接AP,延长BC至点Q,使 CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)∠APC=α,求∠AMQ的大小(用含α的式子表示);
(2)在(1)的条件下,过点M作ME⊥QB于点E,试证明 PC 与 ME 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 . 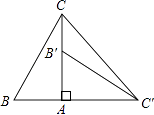
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABDC中,∠ABC的平分线交AD于点E,过点A作BE的垂线交BE于点F,交BC于点G,连接EG,CF.
(1)求证:四边形AEGE是菱形;
(2)若∠ABC=60°,AB=4,AD=5,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com