
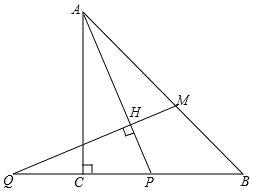
【题目】如图,在等腰Rt△ABC中,角ACB=90°,P是线段BC上一动点(与点B,C不重合)连接AP,延长BC至点Q,使 CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)∠APC=α,求∠AMQ的大小(用含α的式子表示);
(2)在(1)的条件下,过点M作ME⊥QB于点E,试证明 PC 与 ME 之间的数量关系,并证明.
【答案】(1)∠AMQ=45°+α;(2)PC=ME;
【解析】
(1)由等腰直角三角形的性质得出∠BAC=∠B=45°,∠PAB=45°-α,由直角三角形的性质即可得出结论;
(2)由AAS证明△APC≌△QME,得出PC=ME,
(1)∠AMQ=45°+α;理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°-α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°-∠AHM-∠PAB=45°+α;
(2)结论:PC=ME.
理由:连接AQ,作ME⊥QB,如图所示:
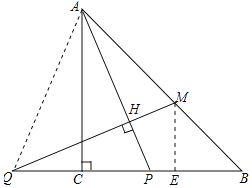
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=45°+α=∠AMQ,
∴AP=AQ=QM,
在△APC和△QME中,
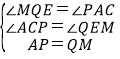 ,
,
∴△APC≌△QME(AAS),
∴PC=ME,


科目:初中数学 来源: 题型:
【题目】为了了解某地九年级学生参加消防知识竞赛成绩(均为整数),从中抽取了1%的同学的竞赛成绩,整理后绘制了如下的频数直方图,请结合图形解答下列问题:
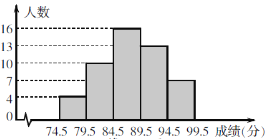
(1)这个问题中的总体是________________;
(2)竞赛成绩在84.5~89.5分这一小组的频率是_____________;
(3)若竞赛成绩在90分以上(含90分)的同学可以获得奖励,则估计该地获得奖励的九年级学生约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
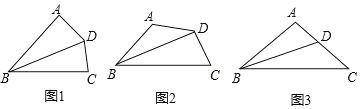
【题目】如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是__________.
(2)问题解决:如图,求证AD=CD;
(3)问题拓展:如图,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线l:y=﹣x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3…按此作法进行去,点A2016的坐标为( )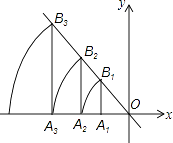
A.(﹣22016 , 0)
B.(﹣22017 , 0)
C.(﹣21008 , 0)
D.(﹣21007 , 0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点 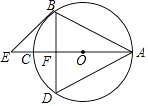
(1)求证:BE为⊙O的切线;
(2)若AF=4CF,求tan∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 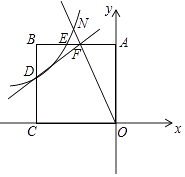
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)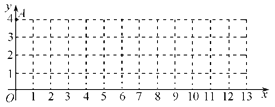
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B分别表示点﹣5、3,M、N两点分别从A、B同时出发以3cm/s、1cm/s的速度沿数轴向右运动.
(1)求线段AB的长;
(2)求当点M、N重合时,它们运动的时间;
(3)M、N在运动的过程中是否存在某一时刻,使BM=2BN.若存在请求出它们运动的时间,若不存在请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com