
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 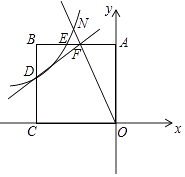
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
【答案】
(1)解:∵S△AOE=3S△OBE,
∴AE=3BE,
∴AE=3,
∴E(﹣3,4)
反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,
(k≠0,且k为常数)的图象过点E,
∴4= ![]() ,即k=﹣12
,即k=﹣12
(2)解:∵正方形AOCB的边长为4,
∴点D的横坐标为﹣4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(﹣4,3).
∵点D在直线y= ![]() x+b上,
x+b上,
∴3= ![]() ×(﹣4)+b,解得b=5.
×(﹣4)+b,解得b=5.
∴直线DF为y= ![]() x+5,
x+5,
将y=4代入y= ![]() x+5,得4=
x+5,得4= ![]() x+5,解得x=﹣2.
x+5,解得x=﹣2.
∴点F的坐标为(﹣2,4),
设直线OF的解析式为y=mx,
代入F的坐标得,4=﹣2m,
解得m=﹣2,
∴直线OF的解析式为y=﹣2x,
解 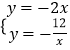 ,得
,得 ![]() .
.
∴N(﹣ ![]() ,2
,2 ![]() )
)
【解析】(1)根据题意求得E的坐标,把点E(﹣3,4)代入利用待定系数法即可求出k的值;(2)由正方形AOCB的边长为4,故可知点D的横坐标为﹣4,点F的纵坐标为4.由于点D在反比例函数的图象上,所以点D的纵坐标为3,即D(﹣4,3),由点D在直线y= ![]() x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标,然后根据待定系数法求得直线OF的解析式,然后联立方程解方程组即可求得.
x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标,然后根据待定系数法求得直线OF的解析式,然后联立方程解方程组即可求得.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】只给定三角形的两个元素,画出的三角形的形状和大小是不确定的,在下列给定的两个条件上增加一个“AB=5cm”的条件后,所画出的三角形的形状和大小仍不能完全确定的是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,角ACB=90°,P是线段BC上一动点(与点B,C不重合)连接AP,延长BC至点Q,使 CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)∠APC=α,求∠AMQ的大小(用含α的式子表示);
(2)在(1)的条件下,过点M作ME⊥QB于点E,试证明 PC 与 ME 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一张长方形纸片,![]() ,
,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() , 则
, 则![]() 等于多少°;
等于多少°;
(3)用含有![]() 、
、![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
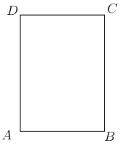
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是 . 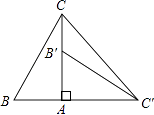
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值.
(1)(2x2y-4xy2)-(-![]() xy2+x2y),其中x=-1,y=2;
xy2+x2y),其中x=-1,y=2;
(2)2x2-[3(-![]() x2+
x2+![]() xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-
xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-![]() |+(y+1)2=0.
|+(y+1)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DECD,正确的有( ) 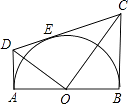
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com