
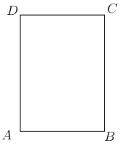
【题目】如图,已知一张长方形纸片,![]() ,
,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() , 则
, 则![]() 等于多少°;
等于多少°;
(3)用含有![]() 、
、![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
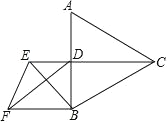
【答案】(1)点F、点E和点G的位置如图所示;见解析;(2)45;(3)![]() .
.
【解析】
依题意先画出图形,再利用折叠的性质来得出等量关系,依次求解.
(1)点F、点E和点G的位置如图所示;
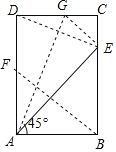
(2)由折叠的性质得:∠DAE=∠EAB,
∵四边形ABCD是矩形,
∴∠BAD=∠DAE+∠EAB=90°,
∴∠EAB=45°;
(3)由折叠的性质得:DG=EG,
∵∠ABE=90°,∠EAB=45°,
∴∠AEB=45°,
∴BE=AB=a,
∴CE=b-a,
设CG=x,则DG=EG=a-x,
在Rt△CEG中,CG2+CE2=EG2,
即x2+(b-a)2=(a-x)2,
解得:x=![]() ,
,
∴DG=a-x=a-![]() =a-b+
=a-b+![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图1,A(m,0),B(0,n),且m,n满足(m﹣2)2![]() 0.
0.
(1)求S△ABO;
(2)点C为y轴负半轴上一点,BD⊥CA交CA的延长线于点D,若∠BAD=∠CAO,求![]() 的值;
的值;
(3)点E为y轴负半轴上一点,OH⊥AE于H,HO,AB的延长线交于点F,G为y轴正半轴上一点,且BG=OE,FG,EA的延长线交于点P,求证:点P的纵坐标是定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线l:y=﹣x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3…按此作法进行去,点A2016的坐标为( )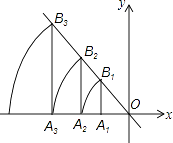
A.(﹣22016 , 0)
B.(﹣22017 , 0)
C.(﹣21008 , 0)
D.(﹣21007 , 0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 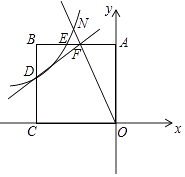
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数x、y满足2x+3y=1.
(1)用含有x的代数式表示y;
(2)若实数y满足y>1,求x的取值范围;
(3)若实数x、y满足x>﹣1,y≥﹣![]() ,且2x﹣3y=k,求k的取值范围.
,且2x﹣3y=k,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.下列说法:①∠BCH=∠CAE;②DF=EF;③CE=BH;④S△ABE=2S△ACE;⑤CF=![]() DF.正确的是_____.
DF.正确的是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com