
【题目】如图1,A(m,0),B(0,n),且m,n满足(m﹣2)2![]() 0.
0.
(1)求S△ABO;
(2)点C为y轴负半轴上一点,BD⊥CA交CA的延长线于点D,若∠BAD=∠CAO,求![]() 的值;
的值;
(3)点E为y轴负半轴上一点,OH⊥AE于H,HO,AB的延长线交于点F,G为y轴正半轴上一点,且BG=OE,FG,EA的延长线交于点P,求证:点P的纵坐标是定值.

【答案】(1)2;(2)![]() ;(3)1
;(3)1
【解析】
(1)利用非负性得出m,n值,即可得出点A,B坐标,最后用三角形的面积公式即可;
(2)先求出先求出OC,进而得出22.5°的正切值,再求出AC的平方,再求出BD的平方即可;
(3)设出点E坐标,用待定系数法和直线交点坐标即可确定出点P坐标即可得出结论.
(1)∵(m﹣2)2![]() 0,∴m=n=2,∴A(2,0),B(0,2),∴OA=2,OB=2,∴S△AOB
0,∴m=n=2,∴A(2,0),B(0,2),∴OA=2,OB=2,∴S△AOB![]() OA×OB=2;
OA×OB=2;
(2)如图1,在OC上取一点E,使OE=OA=2,由(1)知,OA=OB=2,∴∠OAB=45°,∴AE=2![]() .
.
∵∠BAD=∠CAO,∴∠BAD=∠CAO=67.5°.
∵∠ADB=∠AOC=90°,∴∠ABD=∠ACO=22.5°,∴CE=AE=2![]() ,∴OC=OE+CE=2(
,∴OC=OE+CE=2(![]() 1),∴AC2=OA2+OC2=4+4(
1),∴AC2=OA2+OC2=4+4(![]() 1)2=8(2
1)2=8(2![]() ),tan∠ACO
),tan∠ACO![]() 1.
1.
在Rt△ABD中,tan∠ABD=tan22.5°=tan∠ACO![]() 1,∴AD=(
1,∴AD=(![]() 1)BD.
1)BD.
在Rt△AOB中,OA=OB=2,∴AB=2![]() ,根据勾股定理得:AD2+BD2=AB2,∴[(
,根据勾股定理得:AD2+BD2=AB2,∴[(![]() 1)BD]2+BD2=8,∴BD2=2(2
1)BD]2+BD2=8,∴BD2=2(2![]() ),
),![]() ,∴
,∴![]() ;
;
(3)如图2,由(1)知,A(2,0),B(0,2),∴直线AB解析式为y=﹣x+2①,设E(0,a),∴OE=|a|=﹣a.
∵BG=OE,∴BG=﹣a,∴OG=2﹣a,∴G(0,2﹣a).
∵A(2,0),E(0,a),∴直线AE解析式为y![]() x+a②.
x+a②.
∵OH⊥AE,∴直线OH解析式为y![]() x③,联立①③得:x
x③,联立①③得:x![]() ,y
,y![]() ,∴F(
,∴F(![]() ).
).
∵G(0,2﹣a),∴直线FG的解析式为y![]() x+2﹣a④,联立②④得:x
x+2﹣a④,联立②④得:x![]() ,y=1,∴P(
,y=1,∴P(![]() ,1),∴点P的纵坐标是定值,定值为1.
,1),∴点P的纵坐标是定值,定值为1.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.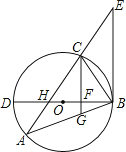
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E,使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断.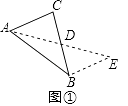
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连结EF.请判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ECF=90°,线段 AB 的端点分别在 CE 和 CF 上,BD 平分∠CBA,并与∠CAB 的外角平分线 AG 所在的直线交于一点 D.
(1)∠D 与∠C 有怎样的数量关系?(直接写出关系及大小)
(2)点 A 在射线 CE 上运动,(不与点 C 重合)时,其它条件不变,(1)中结论还成立吗?说说你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只给定三角形的两个元素,画出的三角形的形状和大小是不确定的,在下列给定的两个条件上增加一个“AB=5cm”的条件后,所画出的三角形的形状和大小仍不能完全确定的是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图2,探究∠CDE与∠B,∠E的数量关系,并说明理由.
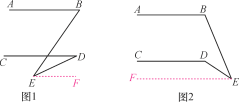
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑩个图形中小圆圈的个数为( )

A. 24 B. 27 C. 30 D. 33
查看答案和解析>>
科目:初中数学 来源: 题型:
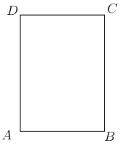
【题目】如图,已知一张长方形纸片,![]() ,
,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() , 则
, 则![]() 等于多少°;
等于多少°;
(3)用含有![]() 、
、![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com