
【题目】已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图2,探究∠CDE与∠B,∠E的数量关系,并说明理由.
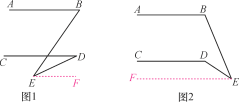
【答案】(1) ∠B=∠BED+∠D. (2)∠CDE=∠B+∠BED.
【解析】
在①中过点E作EF∥AB,由平行线的性质可得∠BEF=∠B,∠D=∠DEF,再根据∠BEF=∠BED+∠DEF等量代换即可得到结果;在②中过点E作EF∥AB,同①的方法,可找到∠BED与∠B、∠CDE的数量关系.
解:(1)∠B=∠BED+∠D.理由如下:
过点E作EF∥AB.
又∵AB∥CD,
∴EF∥AB∥CD.
∴∠BEF=∠B,∠D=∠DEF.
∵∠BEF=∠BED+∠DEF,
∴∠B=∠BED+∠D.
(2)∠CDE=∠B+∠BED.理由如下:
过点E作EF∥AB.
又∵AB∥CD,
∴EF∥AB∥CD.
∴∠B+∠BEF=180°,∠CDE+∠DEF=180°.
又∵∠DEF=∠BEF-∠BED,
∴∠CDE+∠BEF-∠BED=∠B+∠BEF,
即∠CDE=∠B+∠BED.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人都去同一家超市购买大米各两次,甲每次购买50千克的大米,乙每次购买50元的大米,这两人第一次购买大米时售价为每千克m元,第二次购买大米时售价为每千克n元(m≠n),若规定谁两次购买大米的平均单价低,谁的购买方式就合算,则下列观点正确的是( )
A. 甲的购买方式合算 B. 乙的购买方式合算
C. 甲、乙的购买方式同样合算 D. 不能判断谁的购买方式合算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A(m,0),B(0,n),且m,n满足(m﹣2)2![]() 0.
0.
(1)求S△ABO;
(2)点C为y轴负半轴上一点,BD⊥CA交CA的延长线于点D,若∠BAD=∠CAO,求![]() 的值;
的值;
(3)点E为y轴负半轴上一点,OH⊥AE于H,HO,AB的延长线交于点F,G为y轴正半轴上一点,且BG=OE,FG,EA的延长线交于点P,求证:点P的纵坐标是定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20,射线OB的方向是北偏西40,OD是OB的反向延长线,OC是∠AOD的平分线。
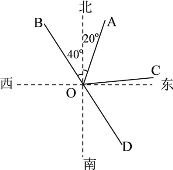
(1)求∠BOC的度数;
(2)求出射线OC的方向。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是全面调查 B. 样本容量是360
C. 该校只有360个家长持反对态度 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B的坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.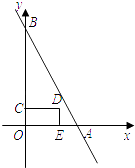
根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,求t的值;
(2)当t=4时,求S的值;
(3)直接写出S与t的函数关系式(不必写出解题过程);
(4)若S=12,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
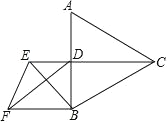
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com