
【题目】在△ABC 中,AD 是高,∠BAD=60°,∠CAD=20°,AE 平分∠BAC,则∠EAD 的度数为_____.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论: ①∠AFC=120°;
②△AEF是等边三角形;
③AC=3OG;
④S△AOG= ![]() S△ABC
S△ABC
其中正确的是 . (把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕
折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的
直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸
片收展平,那么∠AFE的度数为 ( )

A. 60° B. 67.5° C. 72° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E,使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断.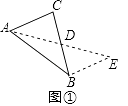
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连结EF.请判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ECF=90°,线段 AB 的端点分别在 CE 和 CF 上,BD 平分∠CBA,并与∠CAB 的外角平分线 AG 所在的直线交于一点 D.
(1)∠D 与∠C 有怎样的数量关系?(直接写出关系及大小)
(2)点 A 在射线 CE 上运动,(不与点 C 重合)时,其它条件不变,(1)中结论还成立吗?说说你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图2,探究∠CDE与∠B,∠E的数量关系,并说明理由.
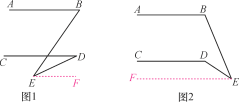
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com