
【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕
折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的
直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸
片收展平,那么∠AFE的度数为 ( )

A. 60° B. 67.5° C. 72° D. 75°
科目:初中数学 来源: 题型:
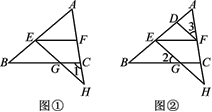
【题目】如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.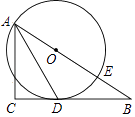
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 ![]() cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以 ![]() cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)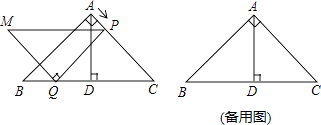
(1)当点M落在AB上时,求x的值;
(2)当点M落在AD上时,PM与CD之间的数量关系是 , 此时x的值是;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20,射线OB的方向是北偏西40,OD是OB的反向延长线,OC是∠AOD的平分线。
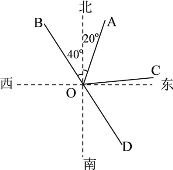
(1)求∠BOC的度数;
(2)求出射线OC的方向。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,E为OP上一点,则下列结论错误的是( )
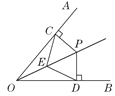
A. CE=DEB. ∠CPO=∠DEPC. ∠CEO=∠DEOD. OC=OD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com